Les secrets du dôme de Florence

Après une enquête approfondie sur les techniques de construction des voûtes et des coupoles depuis l’antiquité jusqu’à nos jours, Karel Vereycken explore et valide la place centrale de la courbe chaînette, une courbe physique, dans la conception du dôme de Florence par Brunelleschi.
Cet article a été initialement publié dans le N°96 de la revue scientifique Fusion de juin 2003 (fichier pdf: Les secrets du dôme de Florence, Fusion). En 2013, Karel Vereycken contribua au numéro hors série « Florence, l’invention de la Renaissance« du magazine Beaux-Arts.
Pour le sage, au contraire, il n’est rien d’invisible, sinon ce qui n’est pas, sinon la pure absence. (Filippo Brunelleschi, en réponse à un de ses détracteurs)
Introduction
Tout le monde pense connaître l’énorme dôme à pans coupés sur plan octogonal de l’église Santa Maria del Fiore dominant la belle ville de Florence de ses quelques cent douze mètres, car chacun l’a vu, au moins en photo.
Le 25 mars 1436, un motet en quatre voix, le Nuper Rosarum Flores composé pour sa consécration par le flamand Guillaume Dufay, annonça : « Naguère des guirlandes de roses, par la grâce pontificale et en dépit d’un hiver sauvage, te furent offertes, Vierge céleste, comme ornement perpétuel, avec un temple de grande ingénuité, à toi dédié avec pitié et sainteté. » (*)
Les deux escaliers de 463 marches qui serpentent entre les deux calottes conduisent à la base d’un lanternon qui se trouve à la hauteur équivalente d’un immeuble de quarante étages. Achevé en 1436 après seize ans et deux semaines de travail acharné, nécessitant près de quatre millions de briques et pesant environ 37.000 tonnes, le dôme est devenu non seulement l’emblème de Florence mais le symbole même de la Renaissance.
Avec ses 42,2 m de diamètre, sa largeur est quasiment l’équivalent de celui de la coupole sphérique du Panthéon de Rome (43,4m) et son diamètre ne sera que légèrement dépassé en 1765 par la Halle aux Blés de Paris (44m). Ni la basilique Saint-Pierre de Rome (42m), ni le dôme des Invalides (27,5m) ni la cathédrale Saint-Paul de Londres (30,7m), ni même la coupole (en métal) du Capitole de Washington D.C. ne le dépassent.
Sa réalisation, tenu pour impossible à son époque, est associée au nom d’un seul homme -Filippo Brunelleschi (1377-1446) – à qui l’on attribue également l’invention de la perspective linéaire. L’architecte, Léon Battista Alberti (1404-1472), dans le prologue de son traité sur la perspective De Pictura (1435) disait de lui : « Quel homme, si dur ou si jaloux, ne louerait l’architecte Filippo en voyant cette énorme construction se dressant jusqu’au ciel, assez vaste pour couvrir de son ombre toute la population de Toscane, et exécutée sans l’aide de poutrages ni de renfort de supports de bois. »
Comme nous allons le voir ici, ce grand chantier, mettant au défi toutes les connaissances humaines de l’époque, fut la véritable locomotive d’une révolution dans les sciences et les techniques qui entraînera, pendant des siècles, une vague d’optimisme au grand bénéfice de l’ensemble de l’humanité.
Avec le duomo, Brunelleschi tracera de nouveaux horizons, bien au-delà de la simple construction d’un édifice.
Qui était Brunelleschi ?
Brunelleschi (Fig. 1) fut le fils d’un notaire de Florence. Doué dès son enfance pour le dessin, son père lui assura une carrière d’orfèvre (orafo). Passionné d’horlogerie et de machines, Brunelleschi eut la chance d’être initié à la géométrie par Paolo Toscanelli del Pozzo (1397-1482) (**), avec lequel il entretint une amitié pendant toute sa vie adulte.
Avec Nicolas de Cuse, Toscanelli, Niccoli, Cesarini et possiblement Brunelleschi, faisaient parti du groupe d’action politique et de réflexion qu’animait le général de l’ordre des Camaldules, Ambrogio Traversari (***) avec l’appui bienveillant de Côme de Medici, grand patron de l’industrie lainière et mécène de la Renaissance.
Cependant, cet engagement n’est pas sans risque. Exploitant politiquement la défaite militaire de Florence contre Lucca de 1433, la famille oligarchique des Albizzi jette tout le blâme sur Côme et le fit jeter en prison, le forçant même en exil à Venise. Ayant perdu son protecteur, Filippo Brunelleschi fut arrêté à son tour sous prétexte de ne pas être à jour avec sa cotisation de membre de la guilde du bâtiment, chose plutôt habituelle à l’époque. Quinze jours plus tard, les Albizzi furent écartés, Filippo relâché et Côme de retour à Florence. Martin V et Eugène IV, qui ouvrit la cathédrale après cent quarante ans de construction, intervinrent personnellement à plusieurs reprises pour protéger et promouvoir l’architecte génial Brunelleschi. Celui-ci, mort en 1446, ne verra ni le lanternon qu’il avait conçu – terminé en 1471- ni la sphère en bronze de 2,5m, fabriquée et posée par l’atelier d’où sortait Léonard de Vinci, celui d’Andrea del Verrocchio.
Genèse du projet
Il fallait enfin achever cet immense chantier sur l’emplacement de l’ancienne église Santa Reparata, commencé en 1296 par Arnolfo di Cambio et agrandi en 1351 par Francesco Talenti. A Florence, tout le monde connaissait bien la forme finale du « dôme à pans coupés sur plan octogonal » à réaliser. Depuis 1367, une maquette du projet était exposée au public dans une des ailes de la Basilique en voie d’agrandissement. Déjà à cette époque, un concours avait opposé deux groupes d’architectes. Le premier, dirigé par Lapo Ghini plaida en faveur d’un concept architectural proche du style gothique traditionnel, combinant des murs assez minces avec un ensemble d’énormes contreforts et arcs-boutants semblables à ceux des cathédrales, destinés à soutenir la coupole.
L’autre groupe, dirigé par l’architecte Neri di Fioravanti, celui qui réalisa la voûte (large de 18m) de la maison d’arrêt Bargello et le Ponto Vecchio. Il exigea, quant à lui, une solution « à l’antique ». Neri, comme beaucoup d’autres en Italie à l’époque, considérait que les arcs-boutants non seulement n’étaient pas très esthétiques mais appartenaient au patrimoine culturel des ennemies traditionnelles des Florentins : les Allemands, les Français, les Milanais et autres « barbares » (Goths).
Selon Neri, on pouvait très bien faire l’économie de ces contreforts et arcs-boutants en incorporant des tirants, en pierre et en bois, autour de la circonférence, semblable à la façon dont les cerceaux cerclent les douves d’un tonneau. Ce concept est intéressant mais, comme nous allons le voir, insuffisant. L’emploi du métal en architecture était encore à un stade assez expérimental. Toutefois, lors de la reconstruction du cœur demi-circulaire de la cathédrale de Beauvais, après son effondrement en 1284, on relia déjà les arcs-boutants entre eux par des tirants en fer afin de renforcer la cohésion de la structure.
Pour la coupole, Neri prévoyait l’utilisation, très rare mais pas exceptionnelle à l’époque, d’une double calotte. Cette technique d’origine Perse est devenue caractéristique des mosquées et des mausolées islamiques, comme le Mausolée à base octogonale de Oljeitü (26m de diamètre) construit en 1309 à Sultanyia (Azerbaïdjan). Une calotte interne porte l’édifice avec sa force structurelle, tandis qu’une calotte externe, en plus d’une protection contre les éléments, permet d’ajouter du volume supplémentaire.
En s’éloignant fortement de la conception du Panthéon de Rome où le dôme sphérique est coincé dans une masse de béton, Neri avait également l’intention d’élever les courbes des pans à élever sous forme d’arcs brisés gothiques, connu en Italie sous le nom de quinto acuto (quinte pointée). Il s’agissait en fait de diviser le diamètre de l’octogone en cinq parties égales, les 4/5ième constituant le rayon de la courbe du dôme (Fig. 2). Après moult débats, le projet de Neri l’emporta et fut dans la foulée approuvé par référendum populaire à Florence. Toutefois , Neri mourut sans laisser aucune instruction précise.
A partir de 1415, tout fut enfin prêt. Avec le tambour nouvellement construit, l’édifice atteignait déjà une hauteur impressionnante de 52 mètres, mais exhibant un trou béant large de plus de 42m. L’heure de la vérité avait sonné.
Antonio di Tuccio Manetti (1423-1497), auteur de La vie de Filippo Brunelleschi, qui a connu Brunelleschi de son vivant, raconte : « D’autant plus que les maîtres d’œuvres s’inquiétaient déjà de la difficulté d’avoir à construire une voûte si large et si haute : étant donné la hauteur et la largeur, donc le poids, les étaiements et soutiens, arcs ou autres armatures, devaient partir de terre, de sorte que, non seulement la dépense leur paraissait effrayante, mais la réalisation à vrai dire absolument impossible. »
A ceux qui évoquèrent cette impossibilité, Brunelleschi répondait que le dôme était un édifice sacré, et que « Dieu, à qui rien n’est impossible, ne nous abandonnerait pas. »
Pour lancer le projet il suggérait aux maîtres d’œuvres, les Fabriciens, d’organiser un colloque international et de réunir tous les architectes, maîtres maçons et ingénieurs « autant qu’on en trouverait dans la chrétienté. »
Cette réunion eut lieu et voici comment Antonio di Tuccio Manetti la relate : « Des paroles de Filippo, les Fabriciens tiraient avec accord le verdict qu’un édifice aussi grand et d’une telle nature ne pouvait être achevé et que ç’avait été une naïveté, de la part des architectes du passé et de ceux qui l’avaient projeté, de le croire. Quand Filippo disait, à l’encontre de cette opinion fausse, qu’on pouvait le faire, ils répondaient tous ensemble : ‘Comment fera-t-on les cintres ?’, mais lui revenait toujours à l’idée qu’on voûterait sans cintre [échafaudage]. Comme ils discutaient la-dessus depuis plusieurs jours, à deux reprises les Fabriciens le firent jeter dehors par des gens à eux et de l’Art de la Laine, comme s’il raisonnait stupidement et ne disait que des paroles ridicules ; au point qu’il lui arriva souvent de raconter que dans ce laps de temps, il n’osait pas se promener dans Florence, ayant l’impression qu’on disait derrière lui : ‘Regarde ce fou qui a de telles prétentions’ »
-

Fig. 3: « l’Âne qui vielle » vous lance d’une façon provocante le défi suivant : le monument que tu contemples est comme une lyre, prête à vibrer sous tes doigts. Sauras-tu en extraire la secrète harmonie, ou bien seras-tu comme moi, l’âne avec ses gros sabots, qui ayant trouvé une lyre, fut incapable d’en jouer…
Dans une autre réunion de travail, et avant d’être nommé capomaestro [architecte en chef] du chantier, on lui demanda d’indiquer sa méthode et les moyens d’exécution qu’il envisageait pour relever ce défi. Craignant qu’on lui vole le projet, Brunelleschi se contenta de leur présenter un oeuf en disant : « Celui qui le fera tenir debout sera digne de faire la coupole. » Après que chacun avait essayé sans succès, Brunelleschi écrasa la pointe de l’œuf sur une table en marbre. Chacun s’écria qu’il en aurait fait autant « s’il avait su », et Brunelleschi répondait en riant qu’ils sauraient également faire la coupole s’il leur montrait son modèle.
Mais en examinant aujourd’hui toutes les solutions créatrices que l’infatigable Brunelleschi aligna pour résoudre les problèmes scientifiques, dans les domaines de la physique, de la géométrie, des machines et des matériaux, sans parler des problèmes politiques, financiers ou de la formation permanente d’une main d’œuvre impliqué dans l’élaboration de technologies révolutionnaires, on doit mesurer la part de courage et de détermination sans laquelle les meilleures idées ne restent que rêveries.
Passionné par le sujet depuis sa tendre enfance, Brunelleschi va imposer des solutions longuement réfléchies. Etant donné qu’excepté un poème, aucun écrit de Brunelleschi ne nous est parvenu, le procédé exact et surtout sa mise en oeuvre resteront un sujet éternel de spéculation. Bien que notre inventeur se battait pour breveter les nouvelles inventions, nous savons que, craignant de se voir dérober sa méthode, il ne communiquait que par des chiffres, et de façon codée.
Ce qui reste à lire est le dôme lui-même, et le spectateur se retrouve un peu comme celui du visiteur de la Cathédrale de Chartres devant l’Ane qui vielle (Fig. 3), cette statue qui vous lance d’une façon provocante le défi suivant : le monument que tu contemples est comme une lyre, prête à vibrer sous tes doigts. Sauras-tu en extraire la secrète harmonie, ou bien seras-tu comme moi, l’âne avec ses gros sabots, qui ayant trouvé une lyre, fut incapable d’en jouer…
Cintrage, ou construire sans bois
Pendant la construction d’un édifice ou d’une coupole, il faut affronter deux forces majeures : d’une part la compression qui provoque un écrasement et, d’autre part, la poussée latérale qui crée une rupture à l’écartement (Fig. 4).
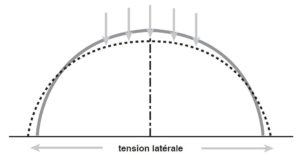
Figure 4. L’architecte doit affronter deux forces majeures : la compression qui provoque un écrasement et la poussée latérale qui crée une rupture à l’écartement.
La compression étant un problème relativement mineur, puisqu’il faut une hauteur importante avant que les pierres du bas ne s’écrasent sous la pression de celles d’en haut, c’est surtout la maîtrise de la pression latérale résultant des poussées verticales qui seront la première préoccupation de l’architecte.
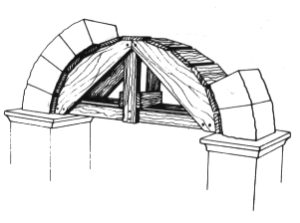
En général, la construction d’arcs s’opérait à partir d’une fausse charpente [supports temporaires] – le cintrage (Fig. 5) – permettant d’élever les voussoirs d’un arc de plein-cintre (roman) ou en arc brisé (gothique).
Ce support n’était retiré qu’après le séchage du mortier, et surtout après la pose de la clef de voûte, laquelle répartissait la poussée sur l’ensemble des voussoirs et la conduisait sur les colonnes qui soutiennent la voûte. Il est indiscutable que, pour des voûtes en berceau ou les nefs gothiques, un cintrage lourd s’avérait indispensable.
Cette technique n’est apparue que très tardivement dans des sociétés capables de produire du bois assez solide, soit au moins d’en disposer. Là, où le bois faisait défaut ou était de mauvaise qualité, on tentait de construire sans cintrage.
Auguste Choisi, dans son Histoire de l’architecture , signale déjà l’existence d’un dôme à Abydos en Egypte où, grâce au limon du Nil, l’emploi de briques crues (argile séchée) auraient permis l’élévation de dômes depuis les premières dynasties pharaoniques (3000 avant J.-C.) (Fig. 6) : « De tous les types de voûtes, celui qui se réalise le plus aisément sans cintres, est la voûte sphérique : le dôme est une des formes usuelles de la voûte égyptienne. Le profil est en ogive ; et la maçonnerie se compose d’assises planes et horizontales, véritables anneaux de briques dont le rayon va sans cesse décroissant. Chaque assise surplombe assez peu sur la précédente pour qu’un support auxiliaire soit superflu. Dès qu’une assise est achevée, elle constitue une couronne indéformable, prête à recevoir en encorbellement une assise nouvelle. »
Nous savons que cette science permettant de bâtir des dômes sans cintrage n’était pas exclusive à l’Egypte, car en remplaçant les briques d’Abydos par des pierres, et en suivant une surface continue, la Grèce mycénienne a pu construire des dômes en « ruches d’abeilles », également exécutés sans cintres, comme celui de la promenade dite « Trésor d’Atrée » dont le diamètre dépasse les 14m (Fig. 7).
-

Figure 7. La Grèce mycénienne a pu construire des dômes en « ruches d’abeilles », également exécutés sans cintres, comme celui de la promenade dite « Trésor d’Atrée » .
Alberti, dans son traité sur l’architecture De re aedificatoria (écrit vers 1440, publié en 1452) affirme que « la voûte sphérique [coupole], unique parmi les voûtes, ne requiert pas de cintrage parce qu’elle n’est pas composé d’arches, mais d’anneaux superposés ».
La plupart des historiens s’accordent aujourd’hui à dire que Brunelleschi, en compagnie de son ami le sculpteur Donatello, a étudié sur place la plupart des monuments que compte Rome.
Pendant plusieurs années, bien avant le concours, les deux amis effectuèrent des relevés de tous les bâtiments et fouillèrent les sous-sols, à tel point qu’on les confondait avec des chasseurs de trésors. Là, ils purent analyser certaines prouesses et faiblesses de l’architecture romaine du IIe siècle en étudiant le Panthéon, (mis en chantier sous Hadrien en 121 après J.C.), le temple de Minerve, ou d’autres bâtiments semblables.
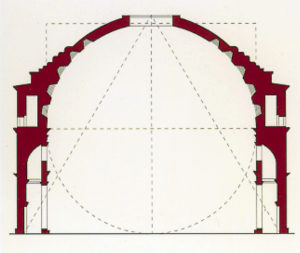
En ce qui concerne le dôme du Panthéon, la calotte intérieure est en réalité soutenue par un énorme contrefort en béton de puzzole (utilisant les cendres du Vésuve) de 5000 tonnes. (Fig. 8). D’environ 44m de diamètre, cette calotte sphérique part de piliers en briques et fait appel à la fameuse « maçonnerie en blocage » (opus caementicium) qui sert de coffrage.
Cette structure est ensuite couronnée par des couches circulaires horizontales de béton. Pour alléger le poids des matériaux, sans porter atteint à leur rigidité, il fut superposé en alternance du béton à la brique, de la brique au tuf et à la toute légère pierre de ponce. Les architectes, dont l’ingéniosité n’avait pas de limite, coulèrent dans le béton des amphores en argile vides pour éviter la surcharge de la voûte.
Par contre, il n’est pas sûr que nos deux artistes aient pu pénétrer dans le Domus Aurea (dôme doré) de Néron, l’emplacement où l’on trouva en 1506 le fameux Laocoon. Néron, après avoir laissé le feu dévaster Rome, fera construire en 64 après J.C. dans sa villa, ce salon à coupole sphérique sur base octogonale d’un diamètre impressionnant de 14m (Fig. 9).
-

Figure 10. La construction sans cintrage à l’époque des cathédrales
La construction sans bois dans un temps moins reculé est aussi documentée dans le livre de John Fitchen The construction of Gothic Cathedrals , qui consacre tout un chapitre aux procédés de construction sans cintrage à l’époque des cathédrales (Fig. 10).
Cependant, les constructeurs firent chaque fois appel à des artifices compliqués intervenant sur le mur « de l’extérieur », sans faire appel à la « géométrie intérieure » de la structure des murs, comme le fera Brunelleschi.
Arcs, voûtes et coupoles
Avec ce survol des techniques de construction sans cintrage il apparaît que la géométrie d’une surface sphérique semble posséder une des qualités fondamentales recherchées par Brunelleschi : l’autosoutènement.
Cette qualité de la courbe est facilement démontrable par une simple expérience. Tout le monde sait qu’une simple feuille de papier A4 de 60 g/m2 ne possède pas la rigidité nécessaire pour soutenir, par exemple, un petit trousseau de clefs. Cependant, si je donne avec ma main une légère courbure à ma feuille, je peux soudainement doter la feuille de cette capacité portante inespérée. Cette force n’appartient pas à la nature de sa matière, mais « émane » du pouvoir de sa structure géométrique.
Avant d’aller plus loin, il est essentiel de s’attarder quelque peu sur les arcs, car certains observateurs prétendent que le dôme de Florence est un mélange de cette science de la construction sphérique « à l’antique » avec le savoir-faire du gothique. Rappelons-le, Neri avait spécifié que les pans devaient s’élever en « quinte pointée », comme les arcs brisés du gothique.
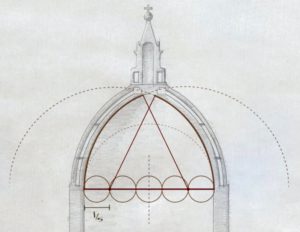
Mais, comme le note Fitchen, p.80 : « Au fur et mesure que le Gothique devenait tardif, un grand nombre de voûtes devenaient de plus en plus pointues, entraînant des problèmes structurels. Dans un système d’arc libre, comme une voûte qui ne porte pas de surcharge et ne fait que se soutenir elle-même, la poussée prend la forme d’une courbe chaînette inversée. Si l’on envisage une chaîne ou un câble librement suspendu entre deux points qui se trouvent à la même hauteur mais séparé par une distance plus petite que la longueur de la chaîne, chaque chaînon possède une unité de poids identique le long du tracée de la chaîne et est en tension avec ses voisins. Ensemble, ses chaînons tracent une ligne courbe dont l’axe est la ligne de la poussée. » (Fig. 11)
-

Figure 11. La construction sans cintrage : grâce à la chaînette, un jeu d’enfant !
Voyons concrètement comment appliquer le principe de la chaînette à l’arc brisé. Si notre arc ne suit (aux extrados ou intrados) le tracé « invisible » de la chaînette, à moins d’être compensé par une rigidité supplémentaire du matériau, nous observons que la poussée provoquera une rupture de l’arc, et les voussoirs du bas, dépourvu de la flexibilité des chaînons, basculeront vers l’extérieur si l’arche est trop pointue, ou s’écrouleront vers l’intérieur si l’arche est faiblement pointue.
En étant plus solide avec moins de matériau, on comprend mieux pourquoi l’arc brisé représente un tel progrès par rapport à l’arc de plein cintre. Bien que beaucoup moins stable, « l’arc chaînette » bénéficie d’une meilleure stabilité statique car harmonique avec le principe physique définissant la gravité. (Fig. 12)

Figure 12. a) Chaque chaînon possède une unité de poids identique le long de la chaînette. b) La poussée sera répartie uniformément
sur un arc qui suit le tracé d’une chaînette inversée.
-

Figure 12 c. c) Si l’arc ne suit pas le tracé « invisible » de la chaînette, à
moins d’être compensé par une rigidité supplémentaire du matériau,
la poussée provoquera une rupture de l’arc.
A partir de l’arc, on peut imaginer la voûte. Des voûtes en berceau ayant la forme d’une chaînette existent, comme l’arc de Ctésiphon (du palais de Taq-i Kisra, près de Baghdad) en Iraq (Fig. 13) (531 après J.-C.), malheureusement endommagé par la crue du Tigre en 1985.
Les lits de briques sont montés à la verticale, voire légèrement inclinés et reposant contre un mur qui absorbe la poussée.
Il est construit sur le même principe que les voutes en berceau, érigées sans cintrage, comme celles du grenier du temple du Ramasséum (Fig. 14), près de Thèbes en Egypte (XIIIième siècle av. J.-C.).
Comprenons bien qu’avec la géométrie de la chaînette utilisée de cette manière, en soumettant l’arc ou la voûte à une poussée qui dépasse son poids propre, il est indispensable d’avoir des renforts. C’est pour cette raison que, dans l’architecture gothique, on utilise des contreforts et des arcs-boutants permettant d’évacuer la poussée s’exerçants sur les murs, contreforts eux-mêmes inscrits de préférence dans les lignes de force d’une… chaînette. (Fig. 15).
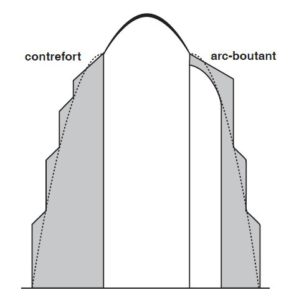
Figure 15. En architecture gothique on utilise des contreforts et des arcs-boutants permettant d’évacuer la poussée s’exerçant sur les murs — contreforts eux-mêmes inscrits de préférence dans les lignes de force d’une… chaînette.
Or, soulignons-le, la voûte construite en forme de chaînette inversée « ne fait que se soutenir elle-même ».
En ce qui concerne le dôme de Brunelleschi, nous avons tenté de connaître les tracés décrits par les huit sproni (éperons en marbre blanc) qui suivent les courbes définies à l’extérieur par l’intersection des pans du dôme. En vain. En effet, les « experts » se disputent sur leur nature exacte – ellipse, tractrice, arc de cercle, chaînette, etc.- et il serait opportun de reprendre les mesures exactes de la construction afin d’avoir une bonne base d’étude.
Par contre, ce que nous savons, c’est l’accusation porté à l’époque contre Brunelleschi par l’un de ses détracteurs, Giovanni Gherardo da Prato, selon laquelle il mettait en danger la construction par son ignorance et pour ne pas avoir respecté la « quinte pointée » comme stipulée dans le contrat.
Da Prato exprima toute sa jalousie dans un poème adressé à Brunelleschi : « O puits profond et noir de totale ignorance, misérable animal, et tellement risible qui veut que l’incertain par chacun soit visible, ton absurde alchimie est sans grande puissance, etc. »
Brunelleschi, qui ne se laissa pas démonter, répondit également par un poème : « Quand le ciel a donné de hautes espérances, ô toi dont l’animale apparence est visible, tout homme peut enfin laisser le corruptible, et disposer en tout d’une grande puissance. Qui mal en juge perd toute son assurance, car il n’affronte rien qui ne lui soit terrible ; pour le sage, au contraire, il n’est rien d’invisible, sinon ce qui n’est pas, sinon la pure absence. L’artiste ne voit pas ces fadaises d’un sot, mais il voit, s’il n’a pas de faux jugements, ce que scelle Nature en dessous son manteau. […] »
Au-delà de l’anecdote, ce poème met bien en évidence la passion de Brunelleschi pour la découverte d’un principe universel invisible qu’il est en train d’arracher aux secrets de la Nature. Comme nous allons le démontrer par la suite, Brunelleschi et ses amis maîtrisaient le principe de la chaînette, et dans le visible et dans l’invisible.
A ce stade, Brunelleschi, chargé de couronner la coupole avec un lanternon pesant plusieurs tonnes, devait écarter les solutions suivantes :
- Les arcs-boutants, il est vrai écartés d’emblée par le contrat, posaient problème car la hauteur de 53m à partir de laquelle il fallait amorcer le dôme rendait inenvisageable l’installation des lourds contreforts qui devaient partir du sol et pour lesquels, de toute façon, il n’y avait plus de place.
- La sphère parfaite constructible sans cintrage par encorbellement de lits de briques était également une fausse voie, car incapable de soutenir le poids du lanternon.
- Un dôme formé par une chaînette en révolution – une caténoïde (Fig. 16) – aurait été lui aussi trop faible pour soutenir la surcharge par sa faible capacité de portance.
-

Figure 16. Un volume formé par une chaînette en révolution – une caténoïde.
Brunelleschi était donc obligé d’inventer la structure et la géométrie physique d’une « surface autoportante », assez légère pour ne pas s’écrouler sous son propre poids, tout en étant assez solide pour porter le lanternon et assez stable pour éviter tout besoin de cintrage.
Les propriétés de la chaînette
Ce fut l’économiste américain Lyndon H. LaRouche qui, en 1988, fut le premier à identifier le principe physique de la chaînette comme étant l’élément fondamental dans la conception du dôme. Toutefois, pour comprendre comment Brunelleschi trouva cette solution, nous devons, probablement comme lui, retourner aux propriétés de la chaînette. C’est en jouant avec celle-ci que l’on peut, éventuellement, en découvrir les propriétés fondamentales :
Équilibre
-

Figure 17. Une corde à deux clous le long d’un mur.
Si on l’accroche une corde à deux clous le long d’un mur (Fig. 17), tout en veillant qu’elle puisse glisser sur les clous pour trouver son propre équilibre, on découvre que la forme de la chaînette dépend presque exclusivement de sa longueur.
Allant à l’encontre de notre bon sens habituel, pour obtenir une chaînette avec un « ventre » plus grand, il faut une corde plus longue, et inversement, pour une courbe de chaînette plus proche de la ligne droite, il faut une plus courte.
Pourquoi ? Parce que la chaînette va chercher son propre équilibre, c’est-à-dire que la somme du poids des parties extérieures va s’égaliser avec le poids de la partie de la chaînette entre les deux clous.
Harmonie préétablie
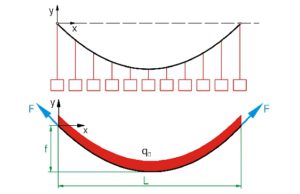
Depuis le début le temps, pour construire des ponts suspendus, l’homme a su utiliser les propriétés de la chaînette, notamment celle de repartir de façon égale sur chaque chainon l’effort à fournir.
Ce principe de répartition égale des tensions, et donc du poids sur l’ensemble des chaînons, fait que si nous déplaçons un petit bout de la chaînette avec notre doigt, la courbe de l’ensemble de la chaînette sera affectée et transformée. Il s’agit de l’expression du principe de moindre action développé par Nicolas de Cuse et Leibniz (****). Il dévoile une « harmonie préétablie » qui fait que n’importe quel évènement à un endroit donné affecte l’ensemble de l’univers, une réalité que la physique Newtonienne est incapable d’expliquer correctement.
Microcosme et macrocosme
-

Figure 18. Si sur une chaînette ACDB, nous relâchons A et B, alors CD reste la même chaînette qu’auparavant.
Le principe précédant fait que chaque bout de chaînette est lui-même une chaînette (Fig. 18), que le macrocosme se reflète dans le microcosme. Si sur une chaînette ACDB, nous relâchons A et B, alors CD reste la même chaînette qu’auparavant. Inversement, selon le même principe, la chaînette (entre ses points de suspension) est définie par n’importe quelles de ses parties, peu importe la taille. De la même façon que le grand se reflète dans le petit, le petit à son tour définit le grand (le microcosme définissant le macrocosme). Dans un sens, si l’on regarde différentes parties d’une chaînette, on regarde différentes expressions locales, d’une réalité globale, harmonieuse et équilibrée.
La sphericam angularem [sphère angulaire]
Avant de poursuivre sur la chaînette, il nous faut approfondir notre concept de surface autoportante. Impressionnée par sa visite du Panthéon, comme le commentaire d’Alberti le reflète, la première approche de Brunelleschi semble avoir été le concept d’une sphericam angularem – une sphère angulaire. Son idée consistait à transférer ou « projeter » les propriétés de solidité inhérente à la géométrie de la sphère sur les huit pans des calottes octogonales.
Ainsi, on pourrait presque dire que la coupole est composé non pas de deux calottes, mais de trois, la troisième étant ce qu’on pourrait appeler une « calotte sphérique imaginaire » (invisible) reliant les deux parois, par un anneau inscrit et circonscrit entre les deux calottes octogonales (Fig. 19).
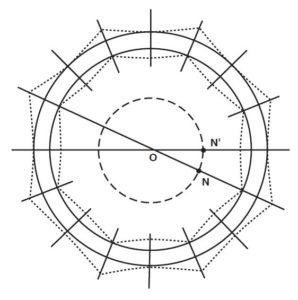
Figure 19. La coupole semble composé non pas de deux calottes, mais de trois. La troisième étant ce qu’on pourrait appeler une « calotte sphérique imaginaire » (invisible) reliant les deux parois par un anneau inscrit et circonscrit entre les deux calottes octogonales.
Quelques années après l’achèvement du dôme, l’architecte Alberti, affirme que l’ « On peut lever des dômes angulaires sans cintrage si vous construisez une [coupole] parfaite (sphérique) à l’intérieur de l’épaisseur de votre ouvrage. Mais là, vous aurez une occasion particulière pour fixer des ligatures afin d’attacher les parties faibles extérieures aux parties fortes de l’intérieur. » (L’art d’édifier, Livre III, Chap. XIV)
Rowland Mainstone, un ingénieur des structures, explique que la calotte intérieure a été construite « comme s’il s’agissait d’une calotte sphérique… mais avec des parties coupées de l’intérieur et de l’extérieur pour respecter la forme octogonale. »
Brunelleschi tenait à l’élévation de cette sphère en hauteur « afin qu’elle sorte encore plus magnifique et dilatée (gonflante) ». Sa forme ne sera pas comme une calotte appuyée sur le corps d’une l’église, mais comme une structure de « crêtes et de voiles » qui se développe en extension et en hauteur.
L’architecte semble aussi vouloir reprendre ici tout un symbolisme traditionnel qui voyait l’action circulaire – expression de la perfection divine – allant à la rencontre de l’action rectiligne – expression de l’imperfection humaine. Nicolas de Cuse, reprenant les défis géométriques et mathématiques lancés par Archimède, creusera ce sujet dans son oeuvre La Quadrature du cercle .
Après tout, une église – maison de Dieu [domus deus] – , ne devait-elle pas être l’espace médiateur entre Dieu et l’homme ? La « sphère » divine, n’allait pas « nous abandonner ». Il devient ainsi clair que Brunelleschi et ses amis ont pu faire la synthèse et « monter sur les épaules » des meilleurs architectes de l’histoire de l’humanité.
Une membrane auto-portante en briques
Quand on monte les escaliers à l’intérieur du dôme, on constate que, sur plusieurs endroits, les motifs de la maçonnerie ont été volontairement laissés visibles (Fig. 20), tandis qu’ailleurs ils sont couverts de crépi. Puisque c’est Brunelleschi qui nous les montre, on a pu en conclure qu’il voulait nous laisser cette piste pour sonder son secret. Néanmoins, ne sous-estimons pas le caractère farceur et illusionniste du personnage, après tout inventeur de la perspective, cette science de l’illusion dont Platon se méfiait tant. Si vous ne voyez pas de l’extérieur les astuces de la construction, ce n’est pas par hasard. Tout Florence fut émerveillée par le dôme et les habitants se demandaient : « Comment est-ce que cela peut-il tenir debout ? Où sont les appuis et soutiens extérieurs ? »
Une analyse de la disposition des quelques 4 millions de briques, dont certains possèdent des formes spéciales (triangulaires, en angle, etc.) et qui sont cachées derrière les lignes droites des tuiles, nous révèle quatre nouveaux concepts importants.
1. Des contreforts invisibles
S’interdisant des contreforts à l’extérieur, Brunelleschi va élaborer tout un dispositif à l’intérieur des parois pour compenser cette absence. Comme spécifié dans son projet déposé aux Œuvres du Dôme (l’original a disparu mais a été copié à l’identique par Manetti) :
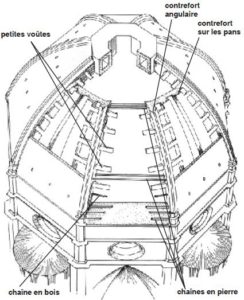
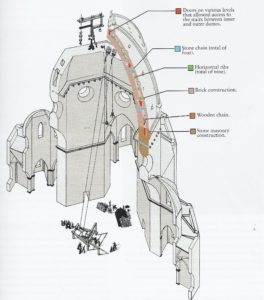
« On fera 24 contreforts [sproni], dont 8 dans les angles et 16 sur les pans ; […] ils devront assembler les deux voûtes et se rétrécir en proportion égale jusqu’en haut de l’ouverture fermée par la lanterne. Lesdits contreforts ainsi que lesdites coupoles seront ceints de 6 cercles [cerchi] de pierre solides, longues et renforcées de fer étamé [reliés avec des crampons] ; au-dessus de ces pierres, des chaînes de fer [catene di ferro, entourées de plomb pour empêcher l’oxydation] entoureront ladite voûte et ses contreforts. » (Fig. 21)
Après avoir spécifié les tailles de tout ces éléments et leurs emplacements exacts, il ajoute : « Mais le premier cercle sera renforcé par des pierres longues en travers, de façon que les deux voûtes de la coupole reposent sur ces pierres. Sur lesdites voûtes, toutes les 12 brasses environ, en hauteur, il y aura des petites voûtes en berceau [volticciuole a botti], d’un contrefort à l’autre, »
Ces « petites voûtes » permettent de renvoyer la pression des huit grands contreforts de façon égale vers les 16 autres et surtout de la repartir sur l’ensemble de la surface qui devient ainsi portante. Et il conclut : « sous ces petites voûtes, d’un contrefort à l’autre, il y aura de grosses chaînes de chêne [catena di quercia] pour assembler les dits contreforts et ceindre la coupole à l’intérieur, et sur ces bois une chaîne de fer [catena di ferro]. Les contreforts seront tous construits en pierre de taille et pierre résistante ; les pans de la coupole seront tous en pierre résistante et assemblés avec les contreforts jusqu’à hauteur de 24 brasses ; au-dessus on construira en brique ou en pierre ponce… »
Bien qu’utilisant les mêmes matériaux que le Panthéon, la réalisation de Brunelleschi se situe néanmoins dans la ligne de Neri di Fioravanti qui nous parlait de « cercler les douves d’un tonneau ». Faute de bois, croît-on, il n’existe dans le dôme qu’une seule chaîne [tirant] en châtaignier, assemblée avec des éléments de fixation en chêne. En réalité cette poutre entourant le dôme, se trouve exactement au point le plus instable de la courbe si elle est mise sous pression. Suite au tremblement de terre de 557 après JC, des tirants en bois furent incorporés dans les bases du dôme Sainte Sophie à Istanbul. Bien que plusieurs tremblements de terre (1510, 1675 et 1895) aient secoué Florence, le dôme a survécu sans problèmes majeurs, grâce à ce dispositif antisismique constitué par ces tirants en pierre solide, en bois et en métal.
Toutefois, pour Brunelleschi, son dôme n’était pas comparable à un tonneau, mais plutôt à un corps humain, fait « d’os et de chair ». Manetti rapportait qu’en étudiant les bâtiments romains, Brunelleschi avait « remarqué la façon de construire des anciens et leur emploi de la symétrie : il identifiait un ordre semblable aux os et à la chair, comme un homme illuminé par Dieu pour les grandes choses. »
Alberti pour sa part affirme que « En ce qui concernent les coupoles, peu importe de quel genre, nous devons imiter la nature, qui, quand elle attache les os, attache la chair avec des nerfs et mêle l’ensemble avec des ligatures et des tendons en longueur, en largeur et en cercles. C’est cette savante disposition qu’il faut imiter dans la construction des arches et coupoles » (L’art d’édifier, Livre III, Chap. XIV)
Les os sont ici les 24 contreforts (comme les côtes du thorax), tandis que les tendons sont en quelque sorte les chaînes. Un squelette équipé de tendons peut-il marcher ? Non, car il reste à définir le muscle qui tient le tout : les briques.
2. Les spirales en Spina Pesce [arêtes de poisson]
Le deuxième concept mobilisé par Brunelleschi sera la disposition des briques dite en spina pesce [arête de poisson], une technique héritée des Etrusques et développée au Trecento toscan. (Fig. 22)
-

Figure 22. La disposition des briques dite en spina pesca [arête de poisson], une technique héritée des Etrusques et développée au Trecento toscan.
L’arête de poisson se forme en alternant à intervalles réguliers la pose horizontale de brique avec une pose verticale. Ces intervalles réguliers sont grands en bas mais décroissent en montant pour disparaître au sommet. Ainsi se forment d’immenses spirales de briques traversant les pans et les contreforts du sommet vers le bas qui répartissant le poids sur la surface portante en expansion.
Ce procédé consiste à dévier le plus possible la poussée du sommet, qui se concentre en principe sur les angles du dôme, vers les « voiles » de la membrane. Une fois de plus, cette technique permet d’induire les propriétés d’une sphère, et notamment la solidité de sa membrane portante, sur les pans fragiles de la coupole octogonale. Avez vous déjà essayé d’écraser un oeuf avec vos deux doigts ? Difficile, sauf si on en casse la pointe sur une table. Peut-être Brunelleschi n’était-il pas si farceur que ça…
3. Le calibrage des briques
Les briques, en réalité d’immenses tuiles, sont orientées d’une façon radiale vers des « points glissants » sur un axe vertical situé au centre du dôme (Fig. 23).
-

Figure 23. Les briques, en réalité d’immenses tuiles, sont orientées d’une façon radiale vers des « points glissants » sur un axe vertical situé au centre du dôme
On pense également que les arêtes saillantes des briques verticales ont pu servir à une équipe chargée de guider les travaux grâce à des fils directeurs ou simbleaux. En vue de l’organisation des échafaudages nécessaires pour permettre aux maçons de se hisser eux-mêmes et les matériaux sur les hauteurs du chantier, on retient l’hypothèse que la coupole a été construite en « anneaux successifs » (Fig. 24).
-

Figure 24. L’on retient l’hypothèse que la coupole a été construite en « anneaux successifs »
Le tracé de la quinte pointée correspond avec l’inclination des briques au sommet qui est de 60 degrés. Si cette inclinaison vers l’intérieur des briques était exclusivement définie à partir d’un point unique au sol, les briques se seraient retrouvées dans une inclinaison proche de 90 degrés, situation fort inconfortable, aussi bien du point de vue structurel que celui du cintrage.
Comme on peut le démontrer sur une maquette, la rotation d’une ficelle d’une longueur donnée, accroché à un point immobile sur le sol du dôme, ne fait que tracer un ensemble de courbes géométriques évolutives – une hyperbole en bas, une parabole au centre et une ellipse en haut – sur les pans de la calotte, à l’instar de la coupe (parabolique) générée par un taille crayon (conique) aiguisant un crayon (hexagonal). On ne peut en aucune manière obtenir la courbe physique – non-algébrique – de la chaînette de cette façon, bien que Brunelleschi utilisa « une perche fixée à la base et tournant sur elle-même vers le haut avec réduction progressive de son inclinaison » pour construire la chapelle de Schiatta Ridolfi, elle, parfaitement sphérique.
4. La Corda da murare [cordeau du maçon]
Finalement, et c’est là que Brunelleschi nous démontre toute sa compréhension de la chaînette, nous devons étudier l’inclinaison en courbe de chaînette des lits de briques entre éperons. Cette inclinaison est parfois stupidement attribuée à l’inattention des ouvriers qui laissent fléchir leur cordeau de maçon, employé pour dresser les parements !
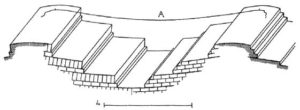
Figure 25. Depuis l’Egypte ancienne, comme dans les murs de l’enceinte d’El Kab, on sait que les lits de briques posées en chaînette font preuve d’une solidité incomparable.
Une fois de plus, depuis l’Egypte ancienne, comme dans les murs de l’enceinte d’El Kab (Fig. 25), on sait que les lits de briques posées en chaînette font preuve d’une solidité incomparable.
La question immédiate qui se pose ici est la suivante : pourquoi utiliser une chaînette orientée vers le bas, et non pas une chaînette inversée, orientée vers le haut, comme toutes les voûtes que nous venons de découvrir ? Eh bien, il semblerait que la chaînette est efficiente dans les deux directions : vers le haut et vers le bas ! Ainsi, les lits de briques en chaînettes créent une contrepoussée permettant de retenir les angles de la coupole, un peu comme le voilage en courbes négatives d’un parapluie qui retient les gaines. Une fois de plus, l’illusionniste Brunelleschi s’amuse à ébranler nos certitudes.
C’est uniquement cette utilisation complexe et scientifique des propriétés de la chaînette qui permirent Brunelleschi de réussir la construction du dôme. « L’harmonie du monde » qui existe entre chaque partie et l’ensemble donna cette qualité d’autosoutènement à l’édifice, tout en assurant sa solidité structurale. Chaque brique (microcosme) construit comme faisant partie d’une chaînette (expression de la moindre action), acquiert les propriétés de la chaînette, c’est-à-dire soutient un poids égal du dôme (macrocosme). A quatre millions de briques, on est plus fort que tous les contreforts de la place. Avec un minimum de matériaux, nous obtenons une surface maximale.
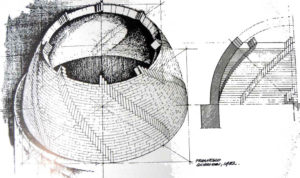
Une maquette (à l’échelle de 1 :5) de la taille d’une maison, construit récemment dans un parc de Florence (Fig. 26) par un architecte passionné, Massimo Ricci, permet de bien voir la maçonnerie en arêtes de poisson. (Fig. 27) Le professeur Ricci, pour sa part, ne croit guère à la chaînette sur laquelle il a peu réfléchi pour l’instant. Il pense qu’il suffit de construire quelques éléments de guidage déduits des courbes d’ellipses d’une forme de fleur, symbole de Santa Maria del Fiore.
Rappelons que même Brunelleschi sera rappelé brutalement à l’ordre par… la chaînette car, pendant l’été 1429, des fissures apparaissent sur les murs latéraux de la partie orientale de la nef. Au lieu de construire des contreforts, Brunelleschi en profite pour imposer le plan d’origine de Neri. Les absides autour de la nef formeront ce qu’il appelait une catena totius ecclesie (une chaîne autour de l’église), capable d’absorber la poussée.
La découverte de l’Amérique
-

Figure 28. La Pinta, une des trois caravelles de Christophe Colomb.
Brunelleschi : perspective linéaire et sphericum angularem , science des coupoles ; Nicolas de Cuse :La Quadrature du Cercle ; le peintre flamand Van Eyck : peinture et un « mappemonde » ; son maître Roger Campin peint des « sorcières », miroirs sphériques ; le miniaturiste Jean Fouquet : la perspective sphérique ; Toscanelli, l’astronomie, la perspective et la cartographie. Si on regarde les domaines divers sur lesquelles ces scientifiques travaillaient, on constate que finalement ils se préoccupaient tous d’un même sujet : la topologie « non linéaire ».
En effet, perspective, optique, cartographie, et les problèmes d’architecture à laquelle était confronté Brunelleschi s’unissent dans une même question : comment les propriétés d’une sphère peuvent-elles se projeter sur un plan ? Et il y avait cette liberté d’esprit, que l’on appelle aujourd’hui pompeusement « la recherche pluridisciplinaire décloisonnée » qui faisait que tout progrès dans un de ces domaines amenait un progrès dans l’autre.
Toscanelli ne souffrait point de ce genre de frustrations. Ross King écrit dans son livre récent « Brunelleschi’s Dome », qu’en 1475, âgé de 78 ans et avec l’accord de l’Oeuvre du Dôme, Toscanelli aurait monté les 463 marches pour installer au sommet du dôme une plaque en bronze, pourvue de petits trous. Grâce àune jauge spéciale sur le sol, un gnomon, Toscanelli fit du dôme le plus grand cadran solaire du monde de cette époque ! Ces observations, destinées officiellement à connaître la date exacte de Pâques, lui permettront de corriger toutes les observations précédentes concernant les équinoxes et les solstices. (Fig. 29)
Or, pour voyager en haute mer avant l’apparition du quadrant et du sextant, on utilisait essentiellement la boussole et l’astrolabe pour mesurer l’angle entre l’horizon et l’étoile polaire. Néanmoins, ces observations ne trouvaient une utilité pratique que grâce à la correction obtenue au moyen des tables d’éphémérides nautiques, en particulier les tables Alphonsines établies en Andalousie sous Alphonse X (le sage) par des astronomes arabes dirigés par le juif Isaac Ben Sid en 1252. Toscanelli correspondait avec Regiomontanus (Johann Müller) de Nuremberg (1436-1476), qui, avec son précepteur, le mathématicien autrichien et ami de Cuse, Georg Peurbach (1423-1461), établiront des nouvelles tables d’éphémérides pour la période de 1475 à 1506. Un élève de Regiomontanus, Martin Behaim (1459-1507) sera le conseiller du roi Jean II du Portugal à Lisbonne, où il a pu croiser Christophe Colomb. Behaim travaillera beaucoup sur les latitudes en mer et fabriquera des astrolabes en cuivre, plus précis que ceux en bois. Le plus ancien globe terrestre que nous connaissons, qui date de 1492, est de sa fabrication.
Ainsi, on peut dire que les observations que Toscanelli effectua sur le toit du dôme de Florence, ont permis l’éclosion d’une nouvelle science. Au-delà de la navigation côtière, renaissait la navigation astronomique. (Fig. 30)
Déjà, dès 1419, année de la découverte de Madère, Henri le Navigateur avait fondé un centre de recherche maritime à Sagres au service des explorateurs portugais. Après la chute de Constantinople en mai 1453, la route de la soie et des épices était fermée en Orient, et l’on chercha des routes passant par le sud en contournant l’Afrique. Mais surtout, Toscanelli avait recueilli les récits de nombreux voyageurs d’extrême orient. En particulier, il a eu un long entretien avec l’ambassadeur du « Cathay » (la Chine). Comme le rapporte Toscanelli lui-même : « A l’époque du Pape Eugène IV [l’époque du Concile de Florence, 1438], un ambassadeur est venu vers lui pour lui exprimer les grands sentiments d’amitié pour les Chrétiens, et j’ai eu une longue conversation avec l’ambassadeur sur beaucoup de questions. »
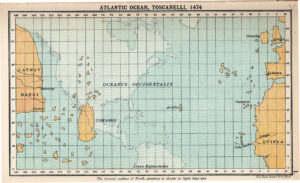
Le 25 juin 1474, Toscanelli envoie sa fameuse lettre avec une carte, à un ami à Lisbonne, le chanoine Fernan Martinez de Roriz qu’il avait rencontré lors du concile à Florence. Martinez figure d’ailleurs avec Toscanelli dans le dialogue scientifique de Nicolas de Cuse La quadrature du Cercle.
Dans cette lettre, Toscanelli lui assurait que le chemin le plus court pour voyager vers le Cathay, à l’est, passait par l’ouest. Martinez, confesseur du roi du Portugal ne réussit pas à convaincre son souverain, mais quelqu’un de sa famille, un jeune capitaine de bateau génois, Christophe Colomb, lequel avait vu passer la lettre et allait écrire à Toscanelli vers 1480. Bien que le vaillant Colomb prétendit ne jamais avoir eu recours à des mathématiques ou une carte, dans ses bagages se trouvait une carte de Toscanelli et très probablement les tables d’éphémérides obtenues grâce au cadran solaire du dôme.(Fig. 31)
Au-delà de la découverte de l’Amérique, la navigation astronomique deviendra une science capable d’en découvrir des milliers. Ainsi le chantier du dôme ne se limitait pas à 37 000 tonnes de briques ou à un simple objet de contemplation esthétique, mais son « âme immortelle » provoqua une vague de révolutions scientifiques de par la planète dont chacun pourra encore bénéficier demain.
- A partir des courbes de moindre action, on peut aussi identifier des surfaces et des volumes de moindre action (« surfaces optimales »), très répandu dans la nature. L’expérience la plus simple permettant de les découvrir sont les bulles de savon. On y découvre la courbe chaînette quand on trempe deux anneaux parallèles en fil de fer dans de l’eau savonnée. (Fig. 32)

Figure 32. Bulle de savon formant un « volume optimal » de type caténoïde (une chaînette en révolution).
Elles forment un « volume optimal » de type caténoïde (une chaînette en révolution). Voir aussi Figure 16.
Quand on y trempe une armature reprenant la géométrie du dôme, des surfaces optimales apparaissent sur les pans, c’est-à-dire des surfaces de courbure « négative » (concaves), une géométrie semblable à celle du parapluie, et identique au léger évasement des pans de la coupole, caché derrière les tuiles.
(Fig. 33)
On peut même faire apparaître la « double calotte » du dôme qui se forme à l’instar du petit cube en eau savonneux qui se forme à l’intérieur d’une structure cubique. Tout ceci tend à nous convaincre que Brunelleschi a conçu l’ensemble de la coupole à partir d’un concept unique de volume optimal fondé sur le principe de moindre action, intensément débattus à l’époque dans son entourage immédiat (Cuse, Toscanelli, etc.).
Lyndon LaRouche, remarque qu’ : « Il est assez troublant de découvrir que le principe de la chaînette fut employé aussi tôt (début du quinzième siècle), pas seulement comme une forme, mais comme un principe physique de courbure capable de résoudre le problème autrement insolvable de la construction. » (« On The Issue of Mind Set », EIR, 3 Mars, 2000)
Notes:
- *Guillaume Dufay est probablement né le 5 août 1397 à Beersel près de Bruxelles, sinon à Cambrai où il mourra en 1474. De 1428 à 1437 il est attaché à la chapelle pontificale, à Rome, Florence et Bologne.
- Il donna un nouveau souffle à une technique ancienne, le motet isorythmique. Selon David Fallows, le Nuper rosarum flores est construit « sur deux voix inférieures exposées quatre fois à des vitesses différentes et selon des longueurs proportionnelles : 6 :4 :2 :3 – ce qui correspond aux proportions de la nef, de la croisée, de l’abside et de la hauteur de la coupole de la cathédrale. Le fait que ces deux voix utilisent la même mélodie -l’Introït pour la dédicace d’une église- à deux niveaux de tonalité et avec des rythmes s’interpénétrant, symbolise l’exploit architectural de Brunelleschi : une calotte intérieure encastrée sur une calotte supérieure. Ainsi, de la même façon que nous sommes séduit par la beauté des formes extérieures du dôme, l’effet musical du motet parvient à son effet musical maximum dans les lignes des voies supérieures. »
** Paolo Toscanelli fut sans doute le plus grand scientifique polyvalent de son temps conduisant des recherches dans tous les domaines importants : mathématiques, géométrie, perspective, cosmologie, médecine, astronomie et surtout la géographie appliquée à la cartographie.
Il écrit un traité sur la perspective en 1420 Della Prospectiva , malheureusement perdu, probablement avec l’aide de Brunelleschi qui selon Manetti faisait ses fameuses expériences à la même époque.Il suivit avec Nicolas de Cuse les cours du mathématicien Prosdocimo del Beldomandi à Padoue.
Avant publication, Cues lui envoie le manuscrit de sa première oeuvre mathématique, les Transmutations géométriques de 1445, puis ses Compléments arithmétiques en 1450. Toscanelli fut souvent appelé « Paolo le médecin », parce qu’il couronna ses études avec un doctorat de médecine tandis que Cuse obtenait le titre de doctor decretorum .
Il devient ensuite conservateur de la bibliothèque de Niccolo Niccoli à Florence. Celui-ci fut un des plus ardents collectionneurs de manuscrits de la Renaissance italienne, dont la collection sera le fonds de départ de la fameuse bibliothèque Laurentienne pour devenir le cœur de la bibliothèque Vaticane. Toscanelli sera aussi un ami direct et l’inspirateur du jeune Léonard de Vinci, et c’est à Toscanelli que son ami Nicolas de Cuse dicte ses dernières volontés sur son lit de mort
- *** C’est Ambrogio Traversari, grand protecteur du peintre Piero della Francesca, que recruta Nicolas de Cuse pour organiser avec lui le grand concile oecuménique qui aura finalement lieu à Florence en 1438 pour tenter de sceller la réunification des églises d’Orient et d’Occident.
- Ils imposeront les plus grands papes humanistes de la Renaissance, Martin V, Eugène IV, Nicolas V et Pie II. Réunir Orient et Occident sous un dôme unique, grand et beau, capable d’englober toutes les coupoles de la chrétienté était un puissant symbole et on mesure derrière ce projet tout l’engagement actif d’une myriade d’humanistes.
- On y réfléchit sur la quadrature du cercle, on apprend le grec et l’hébreu pour percer les secrets des écritures, on traduit Archimède, Végèce et Vitruve pour inventer des machines plus performantes, on démarre l’industrie, on produit du papier pour lancer l’imprimerie, on fonde des hôpitaux et des écoles, bref on ne fait pas que parler de Renaissance, on la fait.
****Pierre de Fermat. La courbe de la chaînette, en opposition avec les courbes algébriques, appartient au domaine des courbes physiques, et exprime le principe de moindre action.
Ce principe baptisé « principe d’économie naturelle » par Pierre Fermat (1601-1665), le chemin emprunté par la lumière pour se rendre d’un point donné à un autre est celui pour lequel le temps de parcours est minimum (« principe de Fermat »).
Leibniz (1646-1716), reprenant le principe du minimum/maximum, que Nicolas de Cuse avait déjà identifié en travaillant sur l’isopérimetrie, le formule ainsi : « Il y a toujours dans les choses, un principe de détermination, qu’il faut tirer de la considération d’un maximum et d’un minimum, à savoir que le maximum d’effet soit fourni avec un minimum de dépense. Dans le cas actuel, le temps et le lieu ou, en un mot, la réceptivité ou capacité du monde peut être considérée comme la dépense, c’est-à-dire le terrain sur lequel il s’agit de construire le plus avantageusement, et les variétés des formes dans le monde correspondent à la commodité de l’édifice, à la multitude et à la beauté des chambres…(…)…Ainsi un liquide placé dans un autre, hétérogène, prend la forme qui a le maximum de capacité, à savoir la forme sphérique. Ainsi encore en mécanique ordinaire, de l’action de plusieurs graves concourant entre eux [une chaîne] résulte le mouvement par lequel en fin de compte se réalise la plus grande descente. Et de même que tout les possibles tendent d’un droit égal à exister, en proportion de leur réalité, ainsi tout les poids tendent aussi d’un droit égal à descendre, en proportion de leur gravité ; de même qu’ici se produit le mouvement dans lequel se remarque le maximum de descente de graves, de même le monde qui se réalise est celui qui réalise le maximum de possibles. » ( De la production originelle des choses prise à sa racine ).
En 1691, Leibniz note que Galilée confondait la chaînette avec la parabole, une différence fondamentale démontrée par Joachim Jungius (1585-1657).
Bibliographie :
- Choisy, Auguste : Histoire de l’Architecture ; Bibliothèque de l’image, 1899.
- Chalifoux, Benoît : Réflexions sur le dôme de Brunelleschi, papier de recherche, 2003.
- Director, Bruce : The long life of the Catenary : from Brunelleschi to LaRouche, Fidelio, Summer/Fall 2002.
- Fitchen, John : The Construction of Gothic Cathedrals, University of Chicago Press, 1961.
- Gärtner, Peter : Brunelleschi, Könemann, Cologne, 1998.
- Hammerman, Nora and Rossi, Claudio : The Apollo project of the Golden Renaissance, Brunelleschi’s dome, 21st Century, July-August 1989.
- King, Ross : Brunelleschi’s Dome, Pimlico, Random, Londres, 2003.
- Leibniz, G.W., Opuscules philosophiques choisis, Vrin, Paris 1978.
- McLean, Alick : « L’architecture des débuts de la Renaissance à Florence », dans La Renaissance italienne, Editions de la Martinière/Könemann, Cologne, 1995.
- Mainstone, Rowland J. : Developments in structural form ; MIT press, Cambridge, Mass., 1975.
- Manetti, Antonio : « Vie, fortune et oeuvre de Filippo Brunelleschi », dans Brunelleschi, Ecole Nationale des Beaux Arts, Paris, 1985.
- Marchini, Giuseppe : Le Baptistère et le dôme de Florence, Beccocci , Florence, 1972.
- Matteoli, Lorenzo : Ser Filippo Brunelleschi and the Dome, Nov. 10th, 2002, Internet.
- Murray, Peter : L’architecture de la Renaissance italienne, Thames & Hudson, Londres, 1969.
- Prager, Franck D. and Gustina Scaglia : Brunelleschi, Studies of his technology and inventions, M.I.T., Cambridge Mass., 1970.
- Scarre, Chris : Monuments du monde ancien, Hazan, Paris, 2000.
- Tennenbaum, Jonathan, « How Gauss Determined The Orbit of Ceres », ch.4, Fidelio, Summer 1998.
- Vasari, Georgio : La Vie des Grandes Artistes, Club du Livre, Paris, 1954.