Étiquette : optique
Van Eyck, un peintre flamand dans l’optique arabe

Le texte qui suit résulte d’une conférence, présentée —en tant que représentant de l’Institut Schiller— sur le thème de « La perspective dans la peinture religieuse flamande du XVe siècle » lors du colloque international « La recherche du divin à travers l’espace géométrique », du 26-28 avril 2006, sous la direction de Luc Bergmans, département d’études néerlandaises de l’université de Paris IV-Sorbonne.
Introduction
« La perspective dans la peinture religieuse flamande du XVe siècle ». De prime abord, ce titre peut surprendre. Car, si on attribue universellement au génie des peintres flamands du quinzième siècle la maîtrise de l’huile siccative, leur géométrie spatiale est d’habitude présentée comme le contre-exemple même de la « bonne perspective ». Déconsidérés par Michel-Ange et son fidèle Vasari, les « primitifs » flamands ne seraient jamais sortis d’un modèle médiéval, archaïque et empirique.Car l’a priori « classiciste », de vigueur jusqu’aujourd’hui, stipule que seule la perspective « renaissante », et donc obéissant au canon de la perspective « linéaire », est « juste ».
Selon la tradition, les recherches faites autour de 1415-20 par l’architecte du dôme Filippo Brunelleschi (1377-1446), superficiellement mentionnées par Antonio Tuccio di Manetti quelques 60 années plus tard, auraient permises à Leon Battista Alberti (1404-1472), se proclamant l’héritier intellectuel de Brunelleschi, d’inventer « la » perspective.
Alberti aurait formulé en 1435 dans De Pictura, un livre entièrement dépourvu du moindre graphique, les prémisses d’un canon perspectiviste capable de représenter, ou du moins d’être conforme, avec nos notions modernes d’espace-temps cartésien [1], un espace-temps caractérisé d’« entièrement rationnel, c’est-à-dire infini, continu et homogène », « en un mot d’un espace purement mathématique [dixit Panofsky] » [2]
Longtemps après, dans un dessin du Codex Madrid (Fig. 1), Léonard de Vinci (1452-1519) tentera de décortiquer le fonctionnement de ce modèle. Mais dans le même manuscrit, il démontra d’une façon rigoureuse les limites inhérentes au canon perspectiviste renaissant Albertien.
Le dessin du f°15, v° (Fig. 2) met clairement en évidence le fait que la projection simple des coupes de pyramides visuelles sur un plan provoque paradoxalement l’accroissement de leurs tailles au fur la mesure de leur éloignement du point de vision, tandis que la réalité exigerait exactement le contraire. [3]
Fort de ce constat, Léonard s’interrogea sur la mobilité de l’œil et sur la nature curviligne de la rétine. Refusant d’immobiliser le spectateur sur un point de vision exclusif [4], Leonard tentera par des constructions curvilignes de corriger ces déformations latérales. [5] Jean Fouquet en France et d’autres travailleront dans le même sens.
Mais les arguments puissants de Léonard de Vinci furent ignorés et n’ont pas pu empêcher cette réécriture de l’histoire.
Malgré cette version officielle de l’histoire de l’art, il faut constater qu’à l’époque, les peintres flamands furent portés aux pinacles par les plus grands mécènes et connaisseurs d’art italiens, spécifiquement pour leur capacité de représenter l’espace. Bartolomeo Fazio, vers le milieu du XVe siècle observait que les tableaux de Jan van Eyck, artiste présenté comme le « peintre principal de notre temps », montraient des « minuscules figures d’hommes, les montagnes, les bosquets, les villages et châteaux rendus avec tant d’adresse qu’on les croirait distants de cinquante mille pas les uns des autres ». [6]
Cette réputation fut telle que des grands noms de la peinture italienne n’avaient aucune réticence à reproduire à l’identique des œuvres flamands. Je pense par exemple à la copie du Christ couronné d’épines de Hans Memlinc au musée de Gênes, copié par Domenico Ghirlandajo (Musée de Philadelphie).
Mais le classicisme post-Michel-Ange jugea que la non-conformité de la géométrie spatiale flamande avec la « substance étendu » de Descartes était un crime impardonnable et que toute déviation, toute insoumission au canon perspectiviste « renaissant » les reléguait à la catégorie de « primitifs », comprenons « empiristes », en clair dépourvus de toute culture scientifique.
De nos jours, ironie de l’histoire, ce ne sont presque uniquement que les artistes qui renoncent explicitement à toute forme de construction perspectiviste au bénéfice d’une pseudo naïveté, qui obtiennent le label de la modernité…
En tout cas, les préjugés actuels font qu’on accuse toujours la peinture flamande du XVe d’avoir ignorée la perspective.
C’est pourtant vrai qu’à la fin du XIVe siècle certains tableaux de Melchior Broederlam (vers 1355-1411) ou d’autres de Robert Campin (1375-1444) (maître de Flémalle) montrent au spectateur des intérieurs ou les assiettes et les couverts sur les tables menacent de glisser soudainement par terre.
Il faut néanmoins admettre que chaque fois que l’artiste « ignore » ou fait fi du schéma de la perspective linéaire, il semble le faire plus par choix que par incapacité. Pour obtenir une composition limpide, le peintre privilégie sa mission didactique au détriment de tout autre considération.
Par exemple, dans le Retable de Mérode de Campin (Fig. 3), on voit que la perspective exagérée de la table permet de montrer avec clarté que le vase se situe derrière le chandelier et le livre.
Le Lam Gods [L’agneau mystique] de Jan van Eyck à Gand en est un autre exemple (Fig. 4.).
Jamais tant de figures, avec tant de détail et de présence, pourraient être montré avec une perspective linéaire où les personnages de l’avant plan cachent très souvent ceux qui sont derrière. [7]
Mais l’intention d’approximer un sens crédible d’espace et de profondeur demeure. Si cette perspective semble bancale par sa géométrie linéaire, Campin impose un sens extraordinaire d’espace par son traitement révolutionnaire des ombres.
Comme chaque peintre le sait, on peint la lumière en peignant l’ombre.
Ainsi chez Campin, chaque objet et chaque personnage, fait nouveau et révolutionnaire, s’y trouve exposé à plusieurs sources de lumière, générant une ombre centrale plus foncée comme le fruit des ombres croisées (Fig. 5).
Van Eyck sous influence de l’optique arabe ?
Ce nouveau traitement de l’espace-lumière a été largement ignoré. Pourtant, plusieurs indices nous permettent d’affirmer que cette nouvelle conception fut en partie le fruit de l’influence de la science « arabe », en particulier de ses travaux sur l’optique.
Traduits en latin et étudiés dès le douzième siècle, leurs travaux furent développées en particulier par un réseau de Franciscains qui avait son épicentre à Oxford (Robert Grosseteste, Roger Bacon, etc.) et rayonnait sur Chartres, Paris, Cologne et le reste de l’Europe.
Il est à noter que Jan van Eyck (1395-1441), figure emblématique de la peinture flamande, s’est rendu comme ambassadeur à Paris, à Prague, au Portugal, et aussi en Angleterre.
J’évoque ici donc rapidement trois éléments permettent d’étayer cette hypothèse de l’influence de la science arabe.
La présence de miroirs courbes
Robert Campin (maître de Flémalle) dans les Volets Werl (1438) (Fig. 6) et Jan van Eyck dans les Epoux Arnolfini (1434) (Fig. 7) font chacun apparaître des miroirs convexes de tailles considérables.
On a la certitude aujourd’hui que vitriers et miroitiers furent des membres à part entier de la guilde de Saint Luc, la guilde des peintres. [8]
Mais il est pertinent de savoir que Campin, maintenant reconnu comme ayant animé à Tournai l’atelier où se sont formés les peintres Van der Weyden et de Jacques Daret, travaillait précisément pour les franciscains dans cette ville. Heinrich Werl, commanditaire du retable où figure le miroir, était un éminent théologien franciscain qui enseignait à l’université de Cologne.
Ces miroirs convexes et concaves (ou ardents) furent très étudiés pendant la renaissance arabe du IXe au XIe siècle, en particulier par le philosophe arabe Al-Kindi (801-873) à Bagdad à l’époque de Charlemagne.
Les scientifiques arabes n’étaient pas seulement en possession de la partie principale des travaux helléniques sur l’optique (Optique d’Euclide, Optique de Ptolémée, les œuvres d’Héron d’Alexandrie, d’Anthémius de Tralles, etc.), mais ce fut parfois la réfutation rigoureuse de cet héritage qui allait donner des ailes à la science.
Après le travail décisif de Ibn Sahl (Xe siècle) c’est celui de Ibn Al-Haytam (Alhazen) [9] (Fig. 8) sur la nature de la lumière, sur les lentilles et les miroirs sphériques qui aura une grande influence. [10]
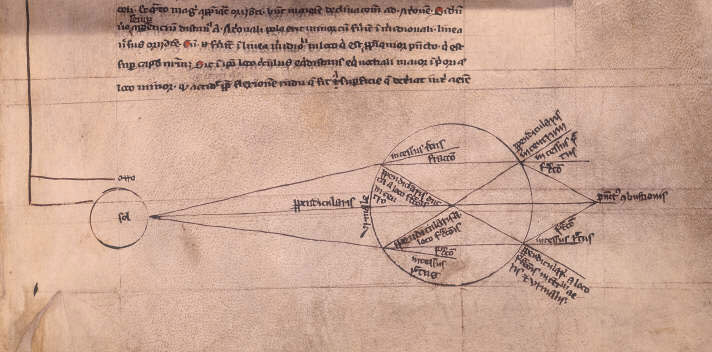
Comme nous l’avons déjà mentionnés, ces études furent reprises par les franciscains d’Oxford, en commençant par l’évêque anglais de Lincoln, Robert Grosseteste (1168-1253). Dans De Natura Locorum Grosseteste montre par exemple un schéma de la réfraction de la lumière dans un verre sphérique rempli d’eau (Fig. 9).
Et dans son De Iride il s’émerveille de cette science :
Cette partie de l’optique, si bien comprise, nous montre comment faire apparaître des choses très lointaines comme si elles étaient situés très proche, et comment on peut faire paraître des choses petites situés à distance à la taille que nous désirons, pour que ça devienne possible pour nous de lire les lettres les plus petites à partir de distances incroyables, ou de compter le sable, ou des grains, ou n’importe quel petit objet.

Son élève Roger Bacon (1212-1292) (Fig. 10) écrit lui-même un traité sur les « Miroirs ardents », le De Speculis Comburentibus reprenant à son tour les travaux d’Ibn Al-Haytam.
Campin, Van Eyck et Van der Weyden montrent fièrement leur connaissance de cette nouvelle révolution scientifique et technologique métamorphosés en symbolismes chrétiens.
Dans leurs tableaux figurent non seulement des miroirs courbes mais aussi des récipients d’eau sphériques (Fig. 11), qu’ils utilisent comme métaphore pour la conception immaculée, car comme le disait une hymne de la Nativité : « Comme, à travers le verre, le rayon passa sans le briser, ainsi de la Vierge Mère, Vierge elle était et vierge elle est demeuré… » [11]
Le traitement de la lumière
Dans son Discours de la lumière, Ibn Al-Haytam développe dans un langage extrêmement poétique sa théorie de la propagation de la lumière en exposant des exigences qui nous rappellent la « révolution Eyckienne ».
En effet, le « réalisme » et la perspective des flamands résultent d’un nouveau traitement de la lumière et de la couleur.
Ibn Al-Haytam :
« La lumière émise par un corps lumineux par lui-même -lumière substantielle- et la lumière émise par un corps éclairé -lumière accidentelle- se propagent sur les corps qui les entourent. ou encore Les corps opaques peuvent être éclairés puis à leur tour émettre de la lumière.
Ce principe physique, dont la théorisation est généralement attribuée à Léonard de Vinci, est omniprésent dans les tableaux flamands.
Il suffit de regarder les images réfléchies dans le casque du Saint-Georges dans la Madone au chanoine van der Paele [12] de Van Eyck (Fig. 12a).
Dans chaque surface courbe du casque de Saint Georges (Fig. 13), on identifie le reflet de la vierge et même une fenêtre à travers laquelle arrive la lumière dans le tableau.
Le bouclier brillant sur le dos de Saint-Georges reflète le socle de la colonne adjacente et le portrait du peintre y figure comme signature. Seul une connaissance de l’optique des surfaces courbes explique ce rendu.
Ibn Al-Haytam : « La lumière peut pénétrer dans les corps transparents : l’eau, l’air, le cristal et leurs homologues. » Et encore :
Les corps transparents ont de même que les corps opaques, une ‘puissance réceptrice’ de lumière, mais les corps transparents ont en outre une ‘puissance transmettrice’ de lumière.
Le développement des médiums huileux et les glacis par les flamands n’est-il pas un écho à ces recherches ? Alternant couches opaques et translucides sur des panneaux très lisses, le médium de l’huile, dans sa spécificité propre, provoque l’altération de l’angle de la réfraction lumineuse.
En 1559, le peintre poète Lucas d’Heere, parlait des tableaux de van Eyck en disant « Ce sont des miroirs, et non des scènes peintes. »
Construction d’une perspective binoculaire
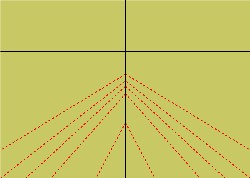
Avant l’arrivée de la perspective linéaire « juste », les historiens d’art ont cherché une cohérence pour expliquer la présence de plusieurs points de fuite d’apparence disparate en théorisant une perspective dite en « arête de poisson ».
Dans ce modèle, un certain nombre de lignes de fuite, au lieu de coïncider dans un seul point de fuite central sur l’horizon, se retrouvent soit dans une « région de fuite » [13](Fig. 14), soit s’alignent sur ce que certains appellent un « axe de fuite » vertical formant ainsi une espèce d’arête de poisson (Fig. 15).
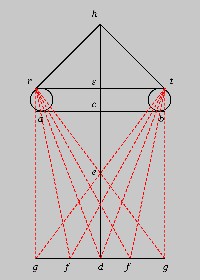
Le professeur Dominique Raynaud [14] remarqua que « tous les traités de perspective du Moyen Age abordent la question de la vision binoculaire », notamment le savant polonais Witelo (1230-1280) [15] dans son Perspectiva (I,27) un savoir également repris d’Ibn Al-Haytam.
Witelo y présente une figure (Fig. 16) pour défendre l’idée que « Les deux formes, qui pénètrent en deux point homologues de la surface des deux yeux, parviennent au même point de la concavité du nerf commun, et se superposent en ce point pour ne faire plus qu’une » (Perspectiva, III, 37).
Un raisonnement similaire apparaît déjà chez Roger Bacon à Oxford et se retrouve dans la Perspectiva Communis de l’archevêque de Canterbury, John Pecham (1240-1290) qui affirme que : « la dualité des yeux doit être ramenée à l’unité ».
Ainsi, comme le proposa le professeur Raynaud, si on prolonge les fameuses lignes de fuites (c’est-à-dire en notre cas les « arêtes de poisson ») jusqu’à ce qu’ils se croisent, le problème de « l’axe de fuite » disparaît car les lignes de fuite se rejoignent.
On obtient alors curieusement une perspective avec deux points de fuite dans la région centrale ! (Fig. 17)
Soudainement les schémas dressés pour démontrer « l’empirisme » des peintres flamands, si on les revoit de ce point de vue, font ressortir une construction légitime probablement conçue à partir de l’optique telle qu’elle fut transmise par la science arabe redécouverte par les réseaux franciscain et d’autres.
Deux tableaux de Jan van Eyck démontrent clairement qu’il a suivi cette démarche : La madone au chanoine van der Paele de 1436 (Fig. 12a, 12b et 12c) et Le tryptique de Dresde de 1437 (Fig. 18a, 18b et 18c).
Est-ce que ce type de perspective fut spécifiquement flamand ? Un examen rigoureux de certains œuvres de Ghiberti, Donatello et Paolo Uccello, généralement datant de la première moitié du quinzième siècle, permet de constater une maîtrise du même principe. (Fig. 19a, 19b)
Nicolas de Cues
Mais toute cette démonstration n’est qu’un regard vers le passé avec les yeux de la rationalité scientifique de notre époque. Il serait une grave erreur de ne pas prendre en compte l’immense influence des « mystiques » rhénans (Maître Eckhart, Johannes Tauler, Heinrich Suso) et flamands (Hadewijch d’Anvers, Jan van Ruusbroec l’Admirable, etc.) .
Ce courant refleuri à partir de la redécouverte du néo-platonisme christianisé de Denis l’Aréopagite (Ve-VIe siècle), rendu accessible par les nouvelles traductions du franciscain Grosseteste à Oxford.
La vision spirituelle de l’Aéropagite, exprimé dans un langage très imagé nous rappelle directement la démarche métaphorique des peintres flamands pour qui un certain type de lumière n’est que la révélation de la grâce divine.
D’emblée l’Aéropagite, dans La Hiérarchie Céleste présente la lumière comme une manifestation de la bonté divine. C’est elle qui nous ennoblit et nous permet d’éclairer les autres :
Que ceux qu’on illumine soient remplis de la divine clarté, et les yeux de leur entendement exercés au travail d’une chaste contemplation ; enfin, que ceux qu’on perfectionne, une fois leur imperfection primitive abolie, participent à la science sanctifiante des merveilleux enseignements qui leur furent déjà manifestés, pareillement, que le purificateur excelle en la pureté qu’il communique aux autres ; que l’illuminateur doué d’une plus grande pénétration d’esprit, également propre à recevoir et à transmettre la lumière, heureusement inondé de la splendeur sacrée, la répande à flots pressés sur ceux qui en sont dignes… [Chap. III, 3]
Repensons de nouveau au Saint-Georges dans la Madone au chanoine van der Paele de Van Eyck qui répand en effet à grands flots les images multiples de la vierge qui l’éclaire.
Ce courant théo-philosophique accèdera à sa pleine maturité dans l’œuvre du cardinal Nicolas de Cues (1401-1464) [16] incarnant la rencontre extrêmement fructueuse de cette « théologie négative » avec la science grecque, le savoir socratique et la renaissance de l’évangélisme chrétien.
A l’opposé à la fois d’une science « sans hypothèse de Dieu » et d’une métaphysique à la dérive ésotérique, un amour tout agapique la porte vers l’éducation du plus grand nombre, vers la défense du faible et de l’humilié. Les Frères et Sœurs de la Vie Commune éduquant Cues et Erasme de Rotterdam en seront le meilleur exemple.
Mais esquissons quelques idées fortes de Nicolas de Cues, relatives à la peinture. Dans De Icona [Le Tableau ou La vision de Dieu] (1453) qu’il envoya au moines bénédictins de la Tegernsee, Cues condense son œuvre fondamental La Docte Ignorance (1440) ou il développe le concept de la coïncidence des opposés. Comme point de départ il prend un autoportrait de son ami, le peintre flamand Rogier van der Weyden, qu’il envoya avec son sermon.
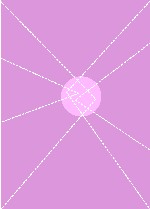
Cet autoportrait, comme des multiples faces du Christ (Fig. 20) peintes au XVe siècle, opère par une « illusion optique » l’effet d’un regard qui fixe le spectateur, peu importe sa position devant le retable.

Dans De Icona, écrit comme un sermon, Cues recommande aux moines de se mettre en demi-cercle autour du tableau et de regarder ce regard qui les poursuit pendant qu’ils se déplacent sur le segment de la courbe. (Voir figure ci-dessus.)
Cues élabore ici un paradoxe pédagogique à partir du fait que le nom grec pour Dieu, Theos, trouve son origine étymologique dans le verbe theastai [voir, regarder]. Vous voyez bien, dit-il, Dieu vous regarde personnellement et son regard vous suit partout. Il est donc un et multiple. Et même quand vous vous détournez de lui, son regard tombe sur vous. Aussi, chose miraculeuse, bien qu’il regarde tout le monde en même temps, il établit néanmoins une relation personnelle avec chacun.
Si « voir » pour Dieu est aimer, le point de vision de Dieu est un amour infini, omniscient et omnipuissant.
C’est ici qu’on peut faire un parallèle avec le miroir sphérique au centre du tableau de Jan van Eyck, Les Epoux Arnolfini (Fig. 7), peint en 1434, dix-neuf ans avant ce sermon.
D’abord ce miroir circulaire (Fig. 21) est bordé des dix stations de la Passion du Christ et juxtaposée par un rosaire, référence explicite à Dieu.
Ensuite, on y découvre une vue de l’ensemble de la pièce, image qui échappe totalement à la perspective linéaire de l’avant plan. Une vue donc comparable à la « vision de Dieu » développée par Cues.
Enfin, on voit dans le miroir deux personnages, mais pas l’image du peintre derrière son chevalet. Il s’agit sans doute des deux témoins du mariage. Au lieu de signer son tableau avec « Van Eyck a fait ceci », le peintre signe ici son tableau au-dessus du miroir avec « Van Eyck a été ici présent » [17] s’identifiant lui-même comme témoin.
Comme l’affirmait Denys l’Aéropagite :
elle [la hiérarchie céleste] transforme ses adeptes en autant d’images de Dieu : purs et splendides miroirs où peut rayonner l’éternelle et ineffable lumière, et qui, selon l’ordre voulu, renvoient libéralement sur les choses inférieures cette clarté empruntée dont ils brillent. » [Chap. III, 2]
Le mystique flamand, Jan van Ruusbroec (1293-1381) évoque une image très similaire dans son Spiegel der eeuwigher salicheit [Miroir du salut éternel] quand il dit « Ende Hi heeft ieghewelcs mensche ziele gescapen alse eenen levenden spieghel, daer Hi dat Beelde sijnre natueren in gedruct heeft. » [Et il créa chaque âme humaine comme un miroir vivant, dans lequel il imprima l’image de sa nature].
Ainsi, comme le miroir, l’âme de Van Eyck, illuminé et vivant dans la vérité de Dieu, prend ici acte comme témoin illuminant cette union. [18]
Ainsi, bien que les peintres flamands du XVe siècle disposaient clairement de bases scientifiques solides, ils choisiront telle ou telle perspective en fonction de l’idée à transmettre.
Leurs tableaux demeureront en essence des objets de spéculation théo-philosophiques capables de louer la bonté, la beauté et la magnificence d’un créateur qui les a créée à son image. Par la nature même de leur démarche, leur intérêt se portait surtout vers la géométrie d’une sorte « d’espace-lumière paradoxale » susceptible par l’énigme à nous ouvrir à une transcendance participative au lieu de chercher à simplement « représenter » un espace mort existant en dehors de la réalité métaphysique.
La seule géométrie digne d’intérêt était celle qui se montrait apte à articuler cette non-linéarité, une perspective « divine » ou « mystique » en mesure de relier la beauté infinie de notre microcosme commensurable avec la bonté incommensurable du macrocosme.
[1] Récemment, des chercheurs italiens ont indiqué le rôle de Biagio Pelacani Da Parma (mort en 1416), professeur à l’université de Padoue près de Venise dans l’imposition d’une telle perspective qui ne privilégiait que les « lois géométriques de l’acte de la vision et les règles du calcul mathématique ».
[2] Erwin Panofsky, La perspective comme forme symbolique, p.41-42, Les Éditions de Minuit, Paris, 1975.
[3] Institut de France, Manuscrit E, 16 v° « l’œil [h] perçoit sur la paroi plane les images des objets éloignés plus grandes que celle de l’objet plus proche. »
[4] Léonard comprend que la perspective Albertienne, telle qu’une anamorphose, condamne le spectateur à se figer sur un point de vision unique et immobile.
[5] Voir notamment le léger agrandissement de la taille des apôtres aux extrémités dans La Cène de Léonard de Vinci au réfectoire de Milan.
[6] Baxandall, Bartholomaeus Facius on painting, Journal of the Warburg and Courtauld Institutes, 27, (1964). Fazio se montre aussi enthousiaste pour une carte du monde de Jan van Eyck, où tous les lieux et régions de la terre sont représentés de façon reconnaissable et à des distances mesurables.
[7] Bruegel, pour échapper à cette fatalité, fera appel à une perspective cavalière plaçant sa ligne d’horizon très haut.
[8] Lionel Simonot, Etude expérimentale et modélisation de la diffusion de la lumière dans une couche de peinture colorée et translucide. Application à l’effet visuel des glacis et des vernis, p.9 (Sujet de thèse, Nov. 2002).
[9] Ibn Al-Haytam (Alhazen) (965-1039) écrivit quelques 200 ouvrages sur les mathématiques, l’astronomie, la physique, la médecine et la philosophie. Né à Bassora, et après avoir travaillé sur l’aménagement des cours du Nil en Égypte, il se serait rendu en Espagne. Il aurait mené une série d’expériences très précises sur l’optique théorique et expérimentale, y compris sur la camera obscura (chambre noire), travaux qu’on retrouve ultérieurement dans les études de Léonard de Vinci. Ce dernier a pu lire les longs passages d’Alhazen qui figurent dans les Commentari du sculpteur florentin Ghiberti. Après que l’évêque de Reims Gerbert d’Aurillac (le futur pape Sylvestre II en 999) ramena d’Espagne le système décimal avec son zéro et un astrolabe, c’est grâce à Gérard de Crémone (1114-vers 1187) que l’Europe va accéder à la science grecque, juive et arabe. Ce savant se rendra 1175 à Tolède pour y apprendre l’arabe et effectuera la traduction de quelques 80 ouvrages scientifiques de l’arabe en latin, notamment l’Almageste de Ptolémée, les Coniques d’Apollonius, plusieurs traités d’Aristote, le Canon d’Avicenne, les œuvres d’Ibn Al-Haytam, d’Al-Kindi, de Thabit ibn Qurra et d’Al-Razi.
[10] Dans le monde arabe, ces recherches furent reprises un siècle plus tard par le physicien persan Al-Farisi (1267-1319). Ce dernier a rédigé un important commentaire du Traité d’optique d’Alhazen. En prenant pour modèle une goutte d’eau et en s’appuyant sur la théorie d’Alhazen sur la double réfraction dans une sphère, il a donné la première explication correcte de l’arc-en-ciel. Il a même suggéré la propriété ondulatoire de la lumière, alors qu’Alhazen avait étudié la lumière à l’aide de balles solides dans ses expériences de réflexion et de réfraction. Désormais la question se posait ainsi : la lumière se propage-t-elle par ondulation ou par transport de particules ?
[11] Meiss, M., Light as form and symbol in some fifteenth century paintings, Art Bulletin, XVIII, 1936, p. 434.
[12] Notez aussi le fait que le chanoine montre une paire de lunettes…
[13] Brion-Guerry dans Jean Pèlerin Viator, sa place dans l’histoire de la perspective, Belles Lettres, 1962, p. 94-96, affirme dans un langage obscure que « l’objet de représentation se comporte le plus souvent chez Van Eyck comme un volume cubique vu de face et par l’intérieur. Le raccourcissement perspectif est obtenu par la construction d’un rectangle dont les cotés constituent la base de quatre trapèzes. Les orthogonales tendent donc vers quatre points de convergence distincts qui forment une ‘région de fuite’ »
[14] Dominique Raynaud, L’Hypothèse d’Oxford, essai sur les origines de la perpective, PUF, Paris 1998.
[15] Witelo était un ami du savant dominicain flamand Willem van Moerbeke, traducteur d’Archimède en contact avec Saint Thomas d’Aquin. Moerbeke était aussi en relation avec le mathématicien Jean Campanus et avec l’astronome néo-platonicien Hendrik Bate van Mechelen.
[16] Cues fut avant tout un homme de science et de théologie. Mais il était aussi un organisateur politique. Le peintre Jan van Eyck se battait pour les mêmes objectifs, comme en témoigne la thématique œcuménique du polyptyque de Gand. On y admire L’agneau mystique, symbole du sacrifice du fils de Dieu pour la rédemption des hommes, capable de réunifier une église déchirée par des différences internes. D’où la présence des trois papes dans le panneau central, ici unis devant l’agneau. Van Eyck exécuta également le portrait du cardinal Niccolo Albergati, un des instigateurs du grand Concile œcuménique organisé par Cues à Ferrare et déplacé à Florence. Si Cues appelait Van der Weyden « son ami Roger », on pense également que Robert Campin a pu le rencontrer, puisqu’il se serait rendu au Concile de Bâle, tout comme un de ses commanditaires, le théologien franciscain Heinrich Werl.
[17] Van Eyck est un des premiers peintres dans l’histoire de l’art à dater et à signer de son nom ses tableaux.
[18] En puisant dans les archives de l’époque, Myriam Greilsammer, dans L’Envers du tableau, Mariage et Maternité en Flandre Médiévale (Editions Armand Colin, 1990) a documenté les frasques sexuelles d’Arnolfini. Ce dernier fut traîné devant les tribunaux par une de ses victimes. Van Eyck semble avoir compris que le chevalier Arnoult Fin, financier lucquois et représentant commercial de la maison Medici à Bruges nécessitait la présence quelque peu particulière de l’œil du seigneur.
Monsieur Hockney, le génie artistique n’est pas une illusion d’optique !

A propos du livre « SAVOIRS SECRETS, Les techniques perdues des maîtres anciens », de David Hockney, Seuil 2001, 295 pages, 65 euros.
Article de ma plume, paru en français en 2001 dans le magazine scientifique Fusion (N° 104), en allemand dans l’hebdomadaire Neue Solidarität et en anglais dans le magazine 21st Century Science & Technology :
FR en PDF: Monsieur Hockney, le génie artistique n’est pas une illusion d’optique
DE en PDF: Kunst ist keine rein technische Fertigkeit
EN as PDF file: Secret Knowledge: Rediscovering the Lost Technique of he Old Masters (p. 59 – 62 of this magazine)