Mercator et la génération Erasme
En 2012, nous célébrons en Belgique où il est né, et en Allemagne où il est décédé à Duisbourg, le 500e anniversaire du fondateur de ce que l’on désigne comme l’école belge de géographie, Gérard Mercator, décédé en 1594 à l’âge de 82 ans.
L’histoire retient qu’il a réussi à projeter la surface du globe terrestre sur un plan, exploit du même ordre que résoudre la quadrature du cercle.
La première raison qui me conduit à parler de Mercator et de son ami et professeur Gemma Frisius (1508-1555), est qu’il s’agit de deux personnalités représentant, et de loin, les esprits les plus créateurs de ce que j’appelle la « génération Erasme de Rotterdam », en réalité le mouvement de jeunes formé par les amis et disciples de ce dernier.
En général, cela étonne car on a fait croire qu’Erasme est un littéraire comique traitant des questions religieuses alors que Frisius et Mercator sont de grands scientifiques. Un cratère lunaire porte le nom de Frisius, un autre celui de Stadius, son élève.
Pourtant, dans un article fort bien documenté [1], le professeur Jan Papy de l’Université de Louvain, a démontré que cette Renaissance scientifique de la première moitié du XVIe siècle, n’a été possible que grâce à une révolution linguistique : au-delà du français et du néerlandais, des centaines de jeunes, étudiant le grec, le latin et l’hébreu, accédèrent à toutes les richesses scientifiques de la philosophie grecque, des meilleurs auteurs latins, grecs et hébreux. Enfin, ils purent lire Platon dans le texte, mais aussi Anaxagore, Héraclite, Thalès, Eudoxe de Cnide, Pythagore, Ératosthène, Archimède, Galien, Vitruve, Pline, Euclide et Ptolémée pour les dépasser ensuite.
Ainsi, dès le XIVe siècle, initié par les humanistes italiens au contact des érudits grecs exilés en Italie, l’examen des sources grecques, hébraïques et latines et la comparaison rigoureuse des grands textes des pères fondateurs de l’Eglise et de l’Evangile, permirent de faire tomber pour un temps la chape de plomb aristotélicienne qui étouffait la Chrétienté et de faire renaître l’idéal, la beauté et le souffle de l’église primitive. [2]
Les Sœurs et Frères de la Vie commune
- Au nord des Alpes, ce sont les Sœurs et Frères de la Vie commune, un ordre enseignant laïc inspiré par Geert Groote (1340-1384), qui ouvriront les premières écoles enseignant les trois langues sacrées. Aujourd’hui, on pourrait croire qu’il s’agissait d’une secte trotskyste puisque l’on changeait son nom d’origine pour un nom latinisé. Gérard (nommé ainsi en l’honneur de Geert Groote) Kremer (cramer ou marchand) devenait ainsi Mercator.
Erasme, lui-même formé à l’école des Frères de la Vie commune de Deventer [3], s’inspira de ce modèle pour fonder en 1517 à Louvain, le fameux Collège Trilingue (Drietongen) qui devint un véritable incubateur d’esprits créateurs. [4]
Pour eux, lire un grand texte dans sa langue originale n’est que la base.
Vient ensuite tout un travail exploratoire : il faut connaître l’histoire et les motivations de l’auteur, son époque, l’histoire des lois de son pays, l’état de la science et du droit, la géographie, la cosmographie, le tout étant des instruments indispensables pour situer les textes dans leur contexte littéraire et historique.
Cette approche « moderne » (questionnement, étude critique des sources, etc.) du Collège Trilingue, après avoir fait ses preuves en clarifiant le message de l’Evangile, se répand alors rapidement à travers toute l’Europe et s’étend à toutes les matières.
Qui était Gemma Frisius ?
Pour bien comprendre l’œuvre de Mercator, une étude de celle de Gemma Frisius s’impose. C’est un jeune orphelin paralysé initialement des jambes, qui est éduqué à Groningen (au nord des Pays-Bas) dans la mouvance que je viens d’évoquer. Ensuite, il est envoyé à l’Université de Louvain (dans le Brabant) au Collège des Lys (de Lelie), où l’on se penche alors depuis un certain temps sur l’humanisme italien. Maître ès arts en 1528, il s’inscrit au Collège Trilingue ou il se lie d’amitié avec des humanistes importants [5], tous rattachés au Collège Trilingue et en relation avec Erasme.
- Féru de mathématiques, Frisius est professeur de médecine, tout en se passionnant pour la cosmographie. Ayant publié une version corrigée de la Cosmographie, une œuvre très populaire du savant saxon, Peter Apianus (1495-1552), il est remarqué par l’évêque Jean Dantiscus (1486-1548), ambassadeur polonais auprès de Charles V. Cet ami d’Erasme, qui deviendra son protecteur, est également en contact avec Copernic.
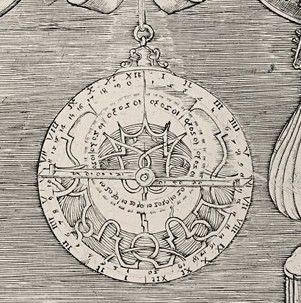
Insatisfait du manque de précision des instruments scientifiques de l’époque, Frisius, bien qu’encore étudiant, crée à Louvain son propre atelier de production de globes terrestres et célestes, d’astrolabes, de « bâtons de Jacob » (arbalestrilles), d’anneaux astronomiques et autres instruments.
- Ces instruments, presque tous des déclinaisons de l’astrolabe inventé par l’astronome grec Hipparque (IIe siècle avant JC, connu par son nom latin Almagestre), permettent à un observateur de localiser sa position sur la surface de la Terre en mesurant l’altitude d’une étoile ou d’une planète par rapport à l’horizon, mais j’y reviens.
Frisius, voulant amener la science au peuple, publie également à Anvers de petits livres expliquant le fonctionnement de chaque instrument. La qualité et la précision exceptionnelle des instruments de l’atelier de Frisius sont louées par Tycho Brahé, et Johannes Kepler, qui retient certaines de ses observations, assimile ses méthodes. Frisius décrit également l’utilisation d’une chambre noire pour observer les éclipses solaires, procédé également repris par Kepler et d’autres astrophysiciens. [6]
Officiellement professeur de médecine à Louvain, Frisius donne des cours privés à des élèves intéressés à la cosmographie.
On ne peut guère douter qu’il fut un excellent professeur puisque quatre de ses disciples deviendront des grands noms de la science belge en réalisant à leur tour des révolutions scientifiques dans leur propre domaine : Gérard Mercator en cartographie, André Vésale (Vesalius) en anatomie, Rembert Dodoens en botanique et Johannes Stadius en astronomie.
Son élève, Mercator
Par exemple, Mercator, né à Rupelmonde entre Anvers et Bruxelles, après une éducation chez les Frères de la Vie commune à ‘s Hertogenbosch, [7] se trouve lui aussi à l’Université de Louvain.
Troublé par la dictature de la pensée aristotélicienne qui y règne, Mercator entre en contact avec Frisius et devient à son tour concepteur d’instruments scientifiques. Formé à la gravure sur cuivre, il assiste Frisius à Anvers et à Louvain dans la fabrication de globes, activité lucrative qui lui garantit par la suite des revenus financiers, essentiels à son indépendance.
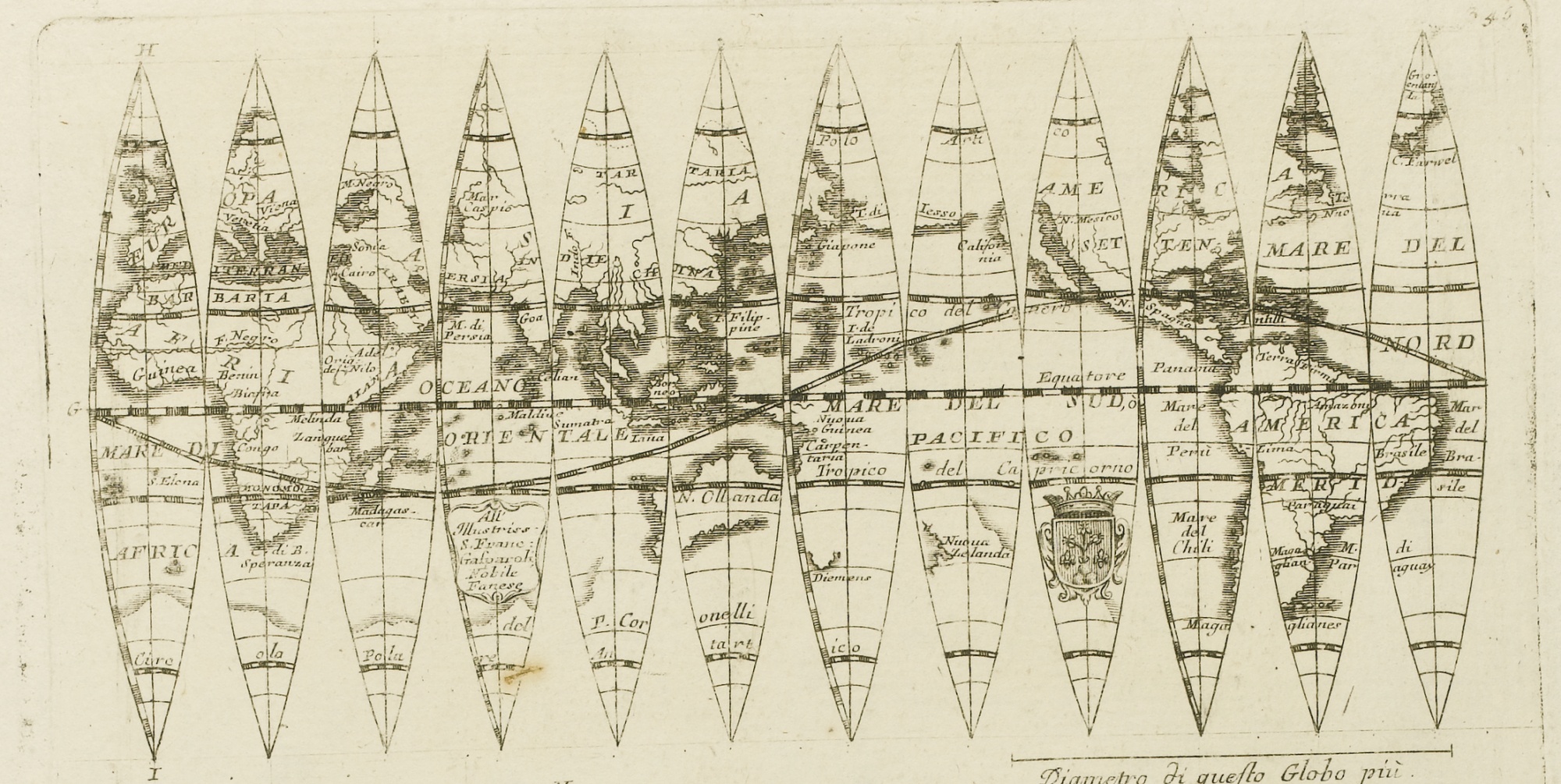
Ensemble, ils produiront des globes d’une précision et d’une élégance remarquable. Au lieu de fabriquer chaque globe à la main comme le faisait avant eux Martin Behaim, ils utilisent le procédé de la gravure. Sur chaque feuille sont imprimés quatre fuseaux d’un globe « déplié », méthode décrite par le peintre et graveur Albrecht Dürer dans son manuel de géométrie. [8] Précisons que Dürer, représentant du cercle de Willibald Pirckheimer à Nuremberg, résida lui aussi jusqu’en 1521 à Anvers.
Une vraie science au-delà du simple témoignage des sens
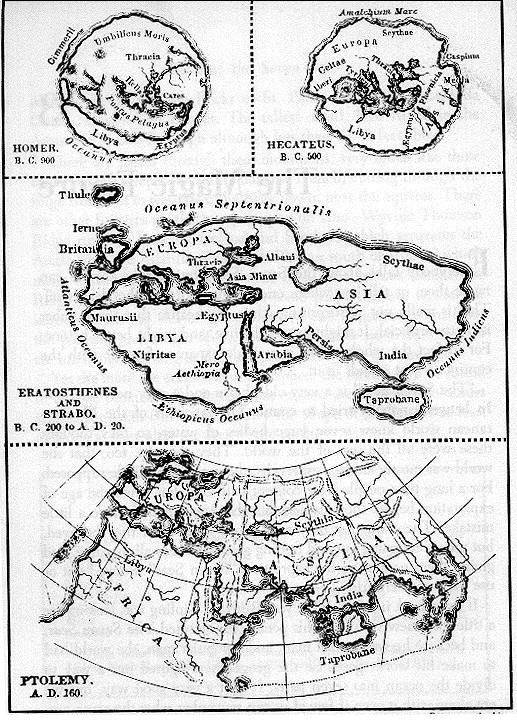
L’astronome romain Claude Ptolémée (IIe siècle), décrit dans sa Geographia un système de coordonnées géographiques définissant les latitudes et les longitudes. En plus, il suggère trois approches pour représenter le caractère sphérique du globe. Depuis Nicolas de Cues, une génération d’humanistes s’est démenée pour reconstituer la carte de Ptolémée absente de ce qui restait de son œuvre.
Leur méthode scientifique représente la deuxième raison pour laquelle nous nous intéressons à ces savants. En retravaillant la science grecque, ils établissent les fondations d’une science libérée de l’empirisme. Car les distances, l’homme a bien du mal à les estimer et il est hors question de les connaître par le sens du gout, par la vue, le toucher, l’odorat ou l’oreille.
Entrons dans le vif du sujet. Imaginez que vous n’ayez ni avion, ni satellite, ni GPS, ni Tom-tom, ni Google maps, et que vous deviez vous situer sur la surface d’un globe. Précisons qu’une bonne carte vous permet de gagner du temps ; elle représente également l’invention de la « marche arrière », c’est-à-dire qu’elle nous permet de revenir sur nos pas.
Or, depuis des millénaires, la cartographie nous lance un double défi.
D’abord, le choix de l’échelle : plus la carte est grande, plus on peut y porter des informations précises. Inversement, plus elle est réduite, plus on perd cette qualité. Pour les instruments de mesure, le même phénomène s’observe. [9]
Ensuite, la précision de la localisation. L’astronome romain Claude Ptolémée (IIe siècle), qui, faisant la synthèse de l’astronomie grecque (Eudoxe de Cnide, Eratosthène, Hipparque, etc.), présente dans sa Geographia un système de coordonnées définissant les latitudes et les longitudes. Un index fournit même les coordonnées de 8000 sites. En Europe, l’œuvre fut publiée pour la première fois à Venise en 1475, sans cartes car aucun exemplaire n’avait survécu au temps. Depuis longtemps, plusieurs savants humanistes, y compris le philosophe-cardinal Nicolas de Cues (1401-1464), avaient tenté de reconstruire la carte de Ptolémée.
Pour savoir où l’homme se trouve à la surface du globe terrestre, il est bien obligé de dépasser le simple témoignage des sens. Bien sûr, les premières cartes marines décrivent des observations faites à partir d’un navire longeant la côte. Pour naviguer en Méditerranée on peut se débrouiller, mais pour traverser un océan et se rendre sur d’autres continents, cette méthode est très risquée. Pour aller en Amérique, ironise-t-on, mettez cap vers le Sud ; arrivé au point où le beurre fond, tournez à droite, ensuite c’est tout droit…
Pour dépasser cette limite, il fallait donc voir plus loin et se repérer sur Terre à partir d’éléments très distants (planètes, étoiles, etc.) ou même à partir de principes physiques invisibles comme par exemple le magnétisme terrestre ou d’autres phénomènes. Après Christophe Colomb, Mercator s’est longuement penché sur la question du champ magnétique terrestre. [10]
Latitudes et longitudes
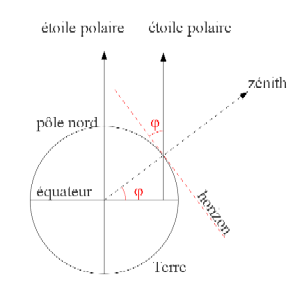
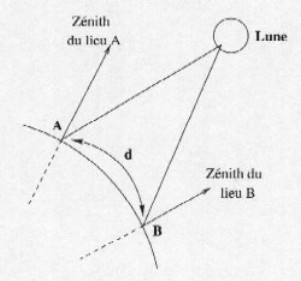
Dans l’hémisphère nord, la méthode la plus simple est de mesurer l’angle formé par l’étoile polaire et l’horizon, car il s’avère que cet angle est égal à l’angle de la latitude, c’est à-dire l’angle formé entre l’équateur, le centre de la terre et l’endroit où l’on se trouve.
L’étoile polaire est (presque) située dans le prolongement exact de l’axe de la Terre et se trouve pour ainsi dire toujours au même endroit au firmament. Dans l’hémisphère Nord, elle apparaît comme le pivot de la voûte céleste. Huit fois plus massive et 1600 fois plus lumineuse que le Soleil, elle est facile à repérer grâce à la constellation de la Grand ourse.
- On peut également trouver sa latitude en observant à midi la hauteur maximale du Soleil, altitude spécifique à chaque jour de l’année pour une latitude donnée. En bref, si l’on connaît la date, on peut connaître sa latitude en consultant un almanach. Ce qui vaut pour le Soleil vaut tout autant pour d’autres astres et étoiles dont on peut mesurer l’altitude. Pour mesurer la latitude, on compte à partir de l’équateur 90° jusqu’au pôle Nord, et 90° jusqu’au pôle Sud.
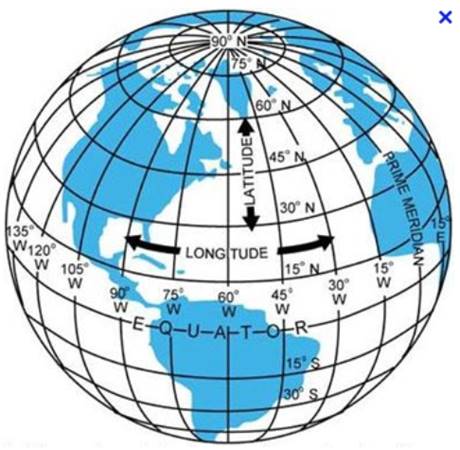 Pour la longitude, c’est beaucoup plus compliqué. D’abord, l’on fait appel à une grille de cercles passant verticalement par les pôles : les méridiens.
Pour la longitude, c’est beaucoup plus compliqué. D’abord, l’on fait appel à une grille de cercles passant verticalement par les pôles : les méridiens.
Comme point de référence, l’on fixe, par simple convention, une méridienne 0.
Ptolémée la faisait passer par les îles Canaries, d’autres par Rhodes, Jérusalem ou encore Paris.
Aujourd’hui, c’est le méridien de Greenwich qui est la méridienne 0 et sert de référence pour les fuseaux horaires.
A partir de cette référence fixée par l’homme, on compte 180° est et 180° ouest. Un degré représente donc 111,11 km à l’équateur, une minute (un soixantième de degré) 1,85 km et une seconde (un soixantième de minute) 30 m.
Ainsi, Bruxelles en Belgique, se trouve sur 50° 51 minutes et 0 seconde nord et 4° 21 minutes et 0 seconde est.
La leçon d’Ératosthène
Pourtant, au IIIe siècle avant JC, Ératosthène avait calculé la circonférence de la Terre avec une remarquable précision.
Il avait observé qu’au solstice d’été, le Soleil éclairait le fond d’un puits à Syène (Assouan) et était donc à la verticale du lieu, ce qui n’était pas le cas à Alexandrie où au même moment un obélisque portait une ombre.
En mesurant l’angle (7,2°) que faisait le soleil à Alexandrie ainsi que la distance entre les deux villes (5000 stades de 157,5 m valent 787,5 km), Ératosthène en déduisit que la circonférence de la Terre (360°) était égale à 250 000 stades (50 arcs de 7,2°, donc 50 x 5000 = 250 000 stades), soit 39 375 km ce qui est très proche de la taille réelle (40 075,02 km).
Comment l’Amérique sauva la vie de Christophe Colomb
Pour illustrer la difficulté du problème des longitudes, prenons l’exemple suivant. L’humaniste italien et ami de Nicolas de Cues, Toscanelli s’est magistralement trompé sur la distance qu’il fallait parcourir pour se rendre au Cathay (Chine) en naviguant vers l’Est, sur la carte envoyée à Christophe Colomb.
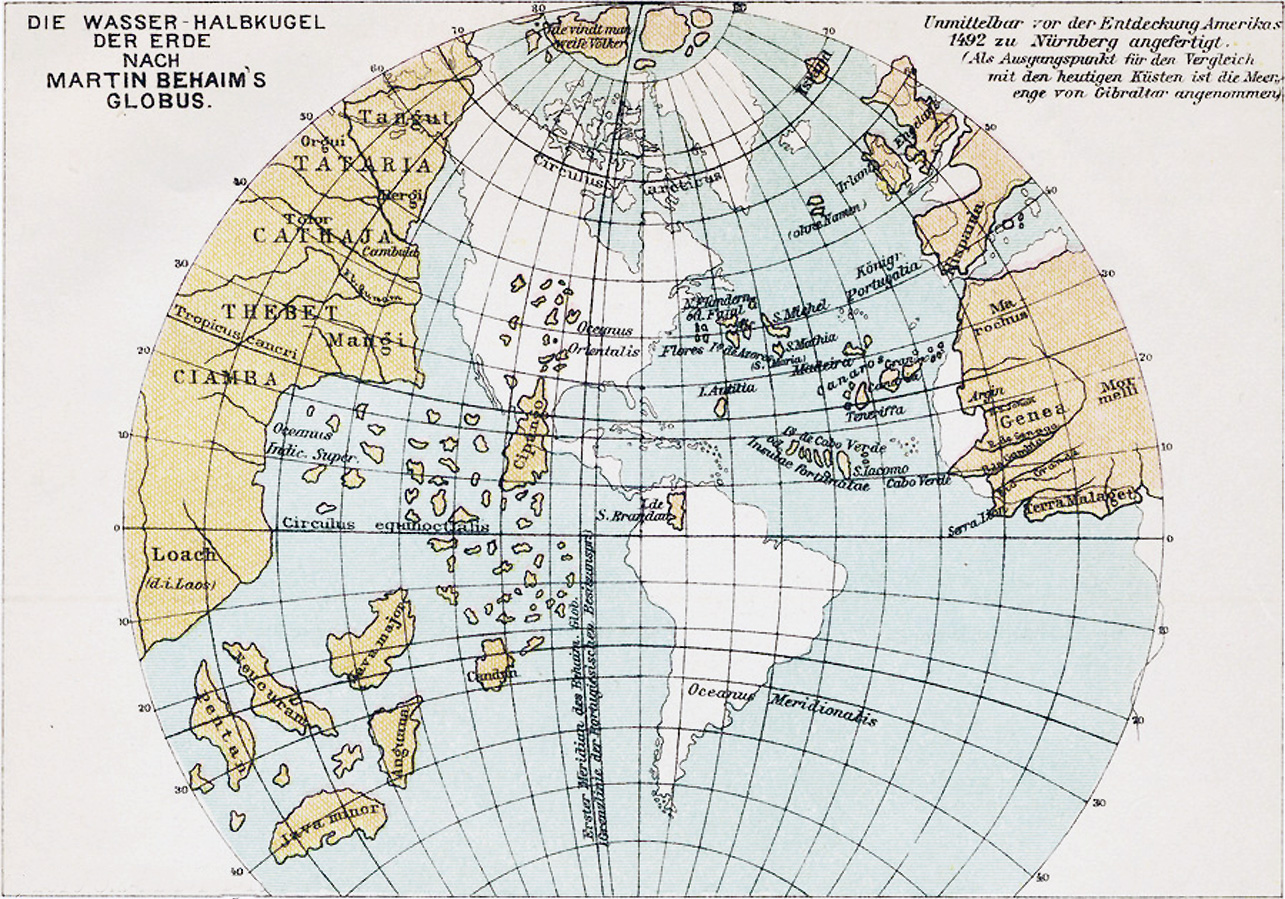
En réalité, Toscanelli a hérité son erreur de Ptolémée qui dans ses calculs sous-estime la circonférence de la Terre. D’autre part, Ptolémée et par la suite Marco Polo, surestiment la longueur du continent eurasiatique. C’est cette vision erronée qu’on retrouve dans le globe réalisé par Martin Behaim à Nuremberg en 1492, le plus ancien globe à nous être parvenu, dont l’année de confection est la même que celle du départ de Colomb et passe pour une bonne illustration du monde tel que l’imaginait Colomb.
Le continent asiatique est développé sur 225 degrés (ce qui « rapproche » l’Europe et l’Asie). La position du Japon (Cipango) placé en fait à la longitude du Mexique raccourcit encore la durée du voyage transocéanique. Une escale aux Canaries, l’espoir de trouver en chemin les îles « Antilles » représentées sur certaines cartes à mi-chemin du Pacifique, l’Asie plus proche qu’elle ne l’est…, c’est ainsi qu’on dit parfois que la carte de Ptolémée a contribué à la découverte du Nouveau Monde…
Ainsi, sur la base des cartes de Marco Polo et d’autres, Toscanelli estime la distance entre Lisbonne et l’Asie à 6500 miles nautiques, soit 9600 km.
Colomb tentera de vérifier cette distance en étudiant les calculs effectués au IXe siècle par Al-Farghani (Alfraganus). Cet astronome persan estimant qu’au niveau de l’équateur, chacun des 360 degrés de la circonférence valent un peu moins de 57 miles, la terre mesure donc 20 400 miles.
C’est alors que Colomb commet une deuxième erreur : Alfraganus travaillait en miles arabes de 1973,5 mètres, Colomb utilise les miles romains de 1481 mètres… pour lui la Terre mesure donc 30 000 kilomètres, 10 000 km de moins que pour Alfraganus ! L’existence imprévue du continent américain, absent de la carte de Toscanelli, a sauvé la vie de Christophe Colomb.
En principe, la solution est relativement simple. Une rotation complète de la Terre dure 24 heures ce qui veut dire qu’en 4 minutes la terre tourne de 1°. Pour connaitre la longitude d’un endroit, il suffit de comparer l’heure locale avec l’heure à l’endroit de la méridienne de référence. Quatre minutes de différence impliquent que l’on est à un degré de distance de celle-ci.
Si le temps mesuré est en avance, cela montre qu’on est à l’Est de la méridienne de référence, on est à l’Ouest si on est en retard. Définir l’heure locale en pleine mer est relativement facile en observant la hauteur des astres, il est en effet midi lorsque le Soleil est au zénith.
Cependant, pour connaître l’heure au niveau de la méridienne de référence, il faut disposer d’une montre réglée sur cette référence.
En 1530, Gemma Frisius est le premier à conceptualiser cette solution, mais à son époque aucune montre n’est assez précise pour mettre en œuvre sa méthode. Il faudra deux siècles, beaucoup de travail à l’Académie des Sciences de Jean-Baptiste Colbert et Christian Huygens et l’invention du chronomètre marin en 1761 par le Britannique John Harrison pour rendre la solution trouvée par Frisius opérationnelle.
Avec la triangulation, la topographie devient une science
-
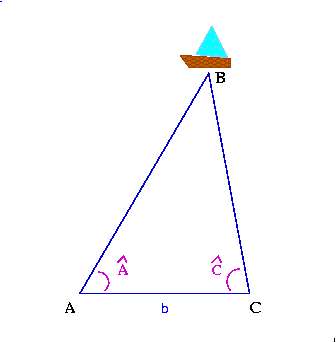
Le principe de la triangulation fut découvert par le savant grec Thalès de Milèt qui s’en servait pour mesurer la distance qui sépare un bateau de la côte en mesurant les angles entre deux points de référence dont on connaît la position et la distance les séparant, et le point dont on souhaite évaluer la distance.
- Frisius fait une autre contribution fondamentale. Dans son Libellus de locorum describendorum ratione, un petit livret d’à peine 16 pages publié en 1533, il décrit la triangulation pour les relevés topographiques, méthode déjà pratiqué par son contemporain Jacob de Deventer et exposé par le mathématicien nurembergeois Régiomontanus (1436-1476) dans son De triangulis omnimodis libri quinque également publié plus d’un demi siècle après sa mort en 1533.
Jusqu’ici nous avons bien vu que la science des angles, puisqu’elle compare des rapports, peut rendre de grands services. Cependant avec la triangulation, on peut aller encore plus loin puisqu’elle établit des rapports entre les longueurs et les angles.
Le principe en fut découvert par Thalès de Milèt qui s’en servait pour mesurer la distance qui sépare un bateau en mer de la côte en mesurant les angles entre deux points de référence dont on connaît la position et la distance les séparant, et le point dont on souhaite évaluer la distance. La triangulation fait appel à la loi des sinus, au fait que la somme des angles d’un triangle est égale à 180 degrés, et aux théorèmes d’Al-Kashi (loi des cosinus) et de Pythagore.
Si aujourd’hui de nombreuses techniques ont remplacé ces calculs mathématiques, la triangulation est encore utilisée par l’armée, lorsque les militaires ne possèdent pas de radar.
Dans son livret, Frisius fait preuve de beaucoup de pédagogie.
Dans un premier temps, il trace sur des feuilles volantes des cercles, avec leur diamètre. Ensuite il grimpe au sommet d’un grand édifice, disons la cathédrale d’Anvers et utilise alors un astrolabe incliné à l’horizontale appelé « cercle entier » ou volcirkel.
L’astrolabe qui permet aux marins de s’orienter par rapport aux étoiles, trouve ici une excellente application terrestre.
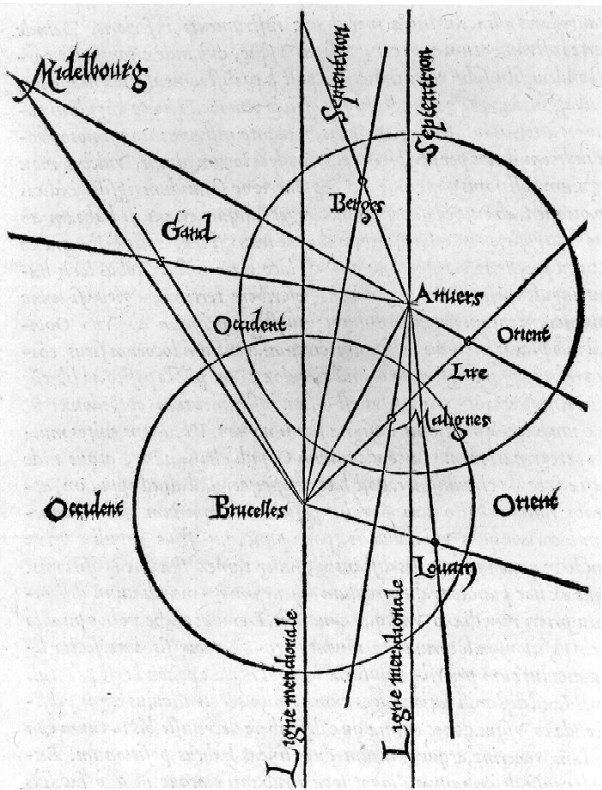
Pour faire un relevé topographique, Gemma Frisius trace d’abord sur des feuilles volantes des cercles avec leur diamètre. Ensuite il grimpe au sommet d’un grand édifice, disons la cathédrale d’Anvers et mesure les angles entre les édifices des villes qu’il observe et l’axe nord-sud qu’indique sa boussole. Ensuite, il se rend dans ces différentes villes et monte aussi dans leurs tours et clochers ayant précédemment servi de repères, afin de répéter l’opération. En rentrant chez lui il place les feuilles à des distances arbitraires entre elles mais toujours en fonction de la méridienne formée par l’axe Nord-Sud. En prolongeant les lignes des différentes directions relevées au sommet des tours, il trouve l’emplacement exact des villes sur les points d’intersection.
Au centre donc de cet astrolabe rebaptisé « cercle entier », Frisius intègre une boussole. Grâce à cet instrument, l’observateur peut maintenant orienter le diamètre de son cercle en papier parallèlement à l’axe Nord-Sud que lui indique la boussole. En vérité, il aligne le diamètre avec une méridienne imaginaire. Ensuite il mesure les angles formés par cette méridienne avec le clocher des églises des environs.
Notons que le relevé topologique publié par Frisius est purement pédagogique car sur le terrain, on ne peut voir les villes indiquées sur son croquis. Cependant, acceptons son exemple.
Nous voyons les directions de Middelburg, Gent, Bruxelles, Louvain, Malines et Lierre, toujours depuis Anvers comme centre.
Ensuite, Frisius descend de sa tour et se rend dans ces différentes villes et monte aussi dans leurs tours et clochers ayant précédemment servi de repères, afin de répéter l’opération.
En rentrant chez lui il place les feuilles à des distances arbitraires entre elles mais toujours en fonction de la méridienne formée par l’axe Nord-Sud.
En prolongeant les lignes des différentes directions relevées au sommet des tours, il trouve l’emplacement exact des villes sur les points d’intersection.
Dans son exemple, il affirme que si l’on octroie quatre unités pour la distance entre Anvers et Malines, on peut ensuite calculer toutes les distances entre les différentes villes.
De Frisius à Colbert
Cette méthode simple et de grande précision fera école. Quand en 1666, Jean-Baptiste Colbert crée l’Académie des sciences, il est persuadé que de meilleures cartes permettront une meilleure gestion et l’aménagement du territoire.
L’abbé Picard, un des cofondateurs de l’Académie utilise la méthode de triangulation de Frisius repris par le mathématicien hollandais Snellius. Il construit une chaîne de treize triangles en partant d’une base mesurée sur le terrain (une deuxième base permettra une vérification) et complétée par des mesures d’angles à partir de points visibles les uns des autres (tours, clochers, …). Picard conçoit lui même ses instruments de mesure et, le premier, utilise une lunette munie d’un réticule.
Dans un autre exemple, l’abbé décrit comment, à partir d’un endroit accessible, à partir d’une longueur connue et un instrument permettant de mesurer les angles, on peut calculer la distance qui nous sépare d’un endroit non-accessible ou distant en utilisant la loi des sinus. On voit immédiatement comment les retombées entre la recherche astronomique et maritime « abstraite » ont rendu beaucoup plus efficace l’organisation de notre environnement immédiat.
Mercator : de la prison à la gloire

En 1544 Mercator passa sept mois dans cette prison (Tour du château de Rupelmonde), soupçonné de ne pas adhérer pleinement aux conceptions aristotéliciennes.
Arrêté pour hérésie en 1544 mais libéré après sept mois de prison, Mercator et sa famille quittent Anvers et les Flandres en 1552 pour s’installer à Duisbourg, petite ville de 3000 habitants dans le duché de Clèves, un « trou » comparé à Anvers où la population dépasse les 100 000 âmes.
S’il habite là-bas, le cosmographe garde le contact permanent avec l’imprimeur anversois Christophe Plantin qui dispose du monopole pour la diffusion des cartes de Mercator pour toute l’Europe et lui fournit régulièrement du papier.
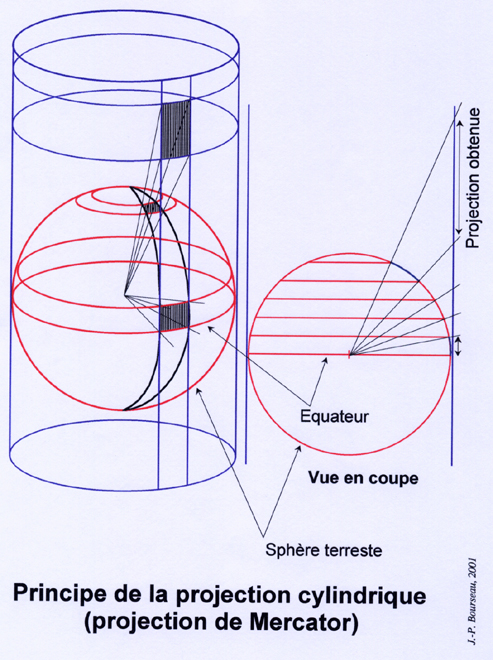
Sur sa carte du monde de 1569 Mercator indique clairement sa méthode de projection : il s’agit de projeter à partir du centre de la sphère chaque point de la surface sur un cylindre. On déroulant ce dernier, l’on obtient la fameuse planisphère.
C’est à Duisbourg que Mercator élabore en 1569 la première carte dite « conforme ».
Bien que sur cette carte les distances ne correspondent aucunement à la réalité (par exemple la taille du Groenland, très au nord, dépasse celle de l’Amérique du Sud sur l’équateur), les rapports angulaires entre les lieux restent exacts.
Alors que les architectes et les géomètres préfèrent des cartes « équidistantes » (1cm sur la carte égale x cm en réalité), les navigateurs préfèrent celle de Mercator.
Lorsque Mercator publie sa carte, son voisin Walther Ghim qui le décrit comme « un homme d’un tempérament calme et d’une candeur et sincérité exceptionnelle » affirme que « Mercator voulait permettre aux savants, voyageurs et marins de voir avec leurs propres yeux une description précise du monde en grand format, projetant le globe sur une surface plane grâce à un moyen adéquat, qui correspondait tellement à la quadrature du cercle que rien ne semblait manquer, comme je l’ai entendu dire de sa propre bouche, si ce n’est la preuve formelle »
Les savants grecs en rêvaient, Mercator l’a fait
Ce dont les savants grecs avaient rêvés et que Frisius avait fixé comme objectif pour la recherche, Mercator l’accomplissait quatorze ans après la mort de son maître.
Dans De Astrolabo Catholico (Anvers, 1556), Frisius a clairement identifié le défi à relever :
« Il est pourtant possible (…) d’obtenir une description sur un plan qui nous donne à voir, dans le plan les mêmes chose que nous appréhendons ailleurs en trois dimensions. Cet artifice, les peintres nous l’exhibent tous les jours, et Albrecht Dürer, ce noble peintre et mathématicien, a mis par écrit de très beaux exemples à ce propos. En effet, il enseigne comment sur une surface plane, qu’il considère comme une fenêtre, n’importe quels objets peuvent être décrits, tels qu’ils apparaissent à l’œil, mais en deux dimensions.
(…) Ptolémée a suivi des principes semblables à la fin du premier livre de sa Géographie, au chapitre 24, dont le titre est : « Comment tracer sur un plan une carte du monde habitée qui soit en harmonie avec son aspect sur la sphère ». Au livre sept également, il propose la même chose plus clairement en ces termes : « Il n’est pas inopportun d’adjoindre quelques directives pour dessiner en plan l’hémisphère que nous voyons et sur lequel se trouve le monde habité, entouré par une sphère armillaire ». En ces endroits, Ptolémée enseigne trois ou quatre manières de transformer la surface vue de la terre habitée sur un plan, de manière à ce que la représentation soit le plus conforme ou similaire à ce qui est décrit sur une surface de forme sphérique, telle qu’on démontre être la surface de la Terre.
Ils existent plusieurs autres méthodes de décrire les cercles de la sphère sur un plan (…), toutes tendant au même but, mais les unes s’approchent plus des rapports sphériques, tandis que d’autres en restent très éloignées. Et bien que Ptolémée dise au premier livre de la Géographie qu’il est impossible que toutes les lignes parallèles conservent les rapports qui existent sur un globe, il est néanmoins possible que toutes les lignes parallèles ne s’écartent pas des rapports qu’ils ont les uns envers les autres et envers l’équateur… »
Mais Gemma, qui semble partager les convictions de Nicolas de Cues sur la quadrature du cercle, insiste sur le fait qu’aucune projection sur un plan ne peut conserver toutes les propriétés de la sphère :
« Mais je veux simplement avertir de ceci : tout ce que nous avons dit ici de la description sur une carte plane sera imparfait si on devait l’examiner en détail. Car jamais on ne pourrait dans un plan réaliser une description des régions qui serait sous tous les aspects satisfaisante, même si Ptolémée revenait. En effet, ou la longitude ne serait pas observée ou la distance ne sera pas respectée, ou l’emplacement serait négligé, ou même deux de ses éléments seraient en défaut, parce qu’il n’y a aucune affinité de la sphère au plan, tout comme il n’en a pas du parfait à l’imparfait ou du fini à l’infini ».
(Postface de 1540 au Libellus sur la triangulation topographique)
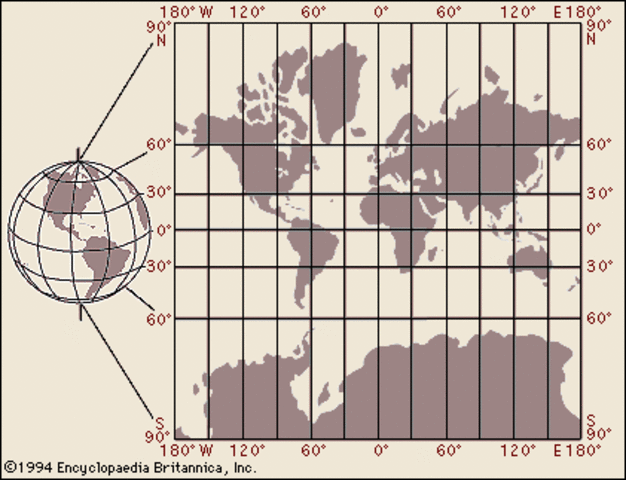
Avec la « Projection de Mercator », les distances ne correspondent aucunement à la réalité (par exemple la taille du Groenland, très au Nord, dépasse celle de l’Amérique du Sud sur l’équateur). Cependant, les rapports angulaires entre les lieux restent exacts (conformes). Alors que les architectes et les géomètres préfèrent des cartes « équidistantes » (1 cm sur la carte égale x cm en réalité), les navigateurs préfèrent celle de Mercator.
Bien que tout indique que Mercator a pu se familiariser avec l’oeuvre de Nicolas de Cues, la méthode scientifique et la solution trouvée par Mercator, c’est-à-dire l’harmonie entre la sphère, le cylindre et le plan, sont souvent présentées comme un mystère, ou le fruit du simple hasard, puisque les équations pour réaliser sa carte datent de beaucoup plus tard.
Ce qui est certain, c’est que, tout comme Johannes Kepler et Leibniz ensuite, il était profondément convaincu que la vie et l’univers n’étaient que le reflet d’’une « harmonie préétablie » et d’un principe créateur.
D’abord, il affirme que « la sagesse, c’est de connaître les causes et les finalités des choses qu’on ne peut pas mieux connaitre que par la fabrique du monde, magnifiquement meublé et conçu par le plus sage architecte d’après les causes inscrites dans leur ordre ».
« J’ai pris un plaisir particulier à étudier la formation du monde comme un tout » écrit-il dans une dédicace. C’est l’orbite suspendu de la Terre, dit-il, « qui contient l’ordre le plus parfait, la proportion la plus harmonieuse et l’admirable excellence singulière de toutes les choses créées ».
Le défi que représentaient les voyages intercontinentaux à l’époque est comparable aux voyages interplanétaires de nos jours.
Il nous faut donc retrouver l’esprit des Frisius et des Mercator pour y parvenir.
Bibliographie :
- Gemma Frisius : Les Principes d’Astronomie et Cosmographie (1556), Kessinger Reprints.
- Fernand Hallyn, Gemma Frisius, arpenteur de la terre et du ciel, Honoré Champion, Paris, 2008.
- John Noble Wilford, The mapmakers, Pimlico, 1981.
- Llyod A. Brown, The Story of Maps, Dover, 1949.
- Gérard Marcel Watelet, Gérard Mercator, cosmographe, Fonds Mercator, 1994, Antwerpen.
- Ann Heinrichs, Gerardus Mercator, Father of Modern Mapmaking, Compass Point Boosks, Minneapolis, 2008.
- Nicholas Crane, Mercator, The Man Who Mapped the Planet, Phoenix 2002.
- Andrew Taylor, The World of Gerard Mercator, Walker & Cie, New York, 2004.
- Mercator, Reizen in het onbekende, Museum Plantin-Moretus, BAI Publishers, Antwerpen, 2012.
- Gerard Mercator en de geografie in de zuiderlijke Nederlanden, Museum Plantin Moretus en Stedelijk prentekabinet, Antwerpen, 1994.
- Le cartographe Gerard Mercator (1512-1594), Crédit Communal, Bruxelles.
- Van Mercator tot computerkaart, Brepols, 2001, Turnhout.
- Recht uit Brecht, De Leuvense hoogleraar Gabriel Mudaeus (1500-1560) als Europees humanist en jurist, Brecht, 2011.